
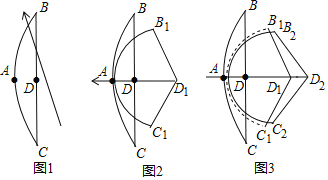
【题目】如图1是小明制作的一副弓箭,点A,D分别是弓臂BAC与弓弦BC的中点,弓弦BC=60cm.沿AD方向拉动弓弦的过程中,假设弓臂BAC始终保持圆弧形,弓弦不伸长.如图2,当弓箭从自然状态的点D拉到点D1时,有AD1=30cm,∠B1D1C1=120°.
(1)图2中,弓臂两端B1,C1的距离为______cm.
(2)如图3,将弓箭继续拉到点D2,使弓臂B2AC2为半圆,则D1D2的长为____cm.
【答案】30![]() 10
10![]() -10
-10
【解析】
(1)如图1中,连接B1C1交DD1于H.解直角三角形求出B1H,再根据垂径定理即可解决问题;
(2)如图3中,连接B1C1交DD1于H,连接B2C2交DD2于G.利用弧长公式求出半圆半径即可解决问题;
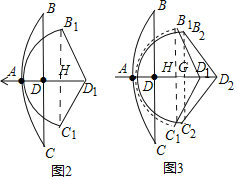
(1)如图2中,连接B1C1交DD1于H.
∵D1A=D1B1=30
∴D1是![]() 的圆心,
的圆心,
∵AD1⊥B1C1,
∴B1H=C1H=30×sin60°=15![]() ,
,
∴B1C1=30![]()
∴弓臂两端B1,C1的距离为30![]()
(2)如图3中,连接B1C1交DD1于H,连接B2C2交DD2于G.
设半圆的半径为r,则πr=![]() ,
,
∴r=20,
∴AG=GB2=20,GD1=30-20=10,
在Rt△GB2D2中,GD2=![]()
∴D1D2=10![]() -10.
-10.
故答案为30![]() ,10
,10![]() -10.
-10.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】定义:若一次函数y=ax+b和反比例函数y=-![]() 满足a+c=2b,则称为y=ax2+bx+c为一次函数和反比例函数的“等差”函数.
满足a+c=2b,则称为y=ax2+bx+c为一次函数和反比例函数的“等差”函数.
(1)判断y=x+b和y=-![]() 是否存在“等差”函数?若存在,写出它们的“等差”函数;
是否存在“等差”函数?若存在,写出它们的“等差”函数;
(2)若y=5x+b和y=-![]() 存在“等差”函数,且“等差”函数的图象与y=-
存在“等差”函数,且“等差”函数的图象与y=-![]() 的图象的一个交点的横坐标为1,求一次函数和反比例函数的表达式;
的图象的一个交点的横坐标为1,求一次函数和反比例函数的表达式;
(3)若一次函数y=ax+b和反比例函数y=-![]() (其中a>0,c>0,a=
(其中a>0,c>0,a=![]() b)存在“等差”函数,且y=ax+b与“等差”函数有两个交点A(x1,y1)、B(x2,y2),试判断“等差”函数图象上是否存在一点P(x,y)(其中x1<x<x2),使得△ABP的面积最大?若存在,用c表示△ABP的面积的最大值;若不存在,请说明理由.
b)存在“等差”函数,且y=ax+b与“等差”函数有两个交点A(x1,y1)、B(x2,y2),试判断“等差”函数图象上是否存在一点P(x,y)(其中x1<x<x2),使得△ABP的面积最大?若存在,用c表示△ABP的面积的最大值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xoy中,A(﹣3,0),B(0,1),形状相同的抛物线Cn(n=1,2,3,4,…)的顶点在直线AB上,其对称轴与x轴的交点的横坐标依次为2,3,5,8,13,…,根据上述规律,抛物线C2的顶点坐标为_____;抛物线C8的顶点坐标为_____.
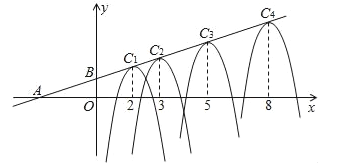
查看答案和解析>>
科目:初中数学 来源: 题型:
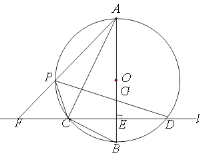
【题目】如图,在⊙O的内接三角形ABC中,![]() ,
,![]() ,过C作AB的垂线l交⊙O于另一点D,垂足为E.设P是
,过C作AB的垂线l交⊙O于另一点D,垂足为E.设P是![]() 上异于A,C的一个动点,射线AP交l于点F,连接PC与PD,PD交AB于点G.
上异于A,C的一个动点,射线AP交l于点F,连接PC与PD,PD交AB于点G.
(1)求证:![]() ;
;
(2)若![]() ,
, ![]() ,求PD的长.
,求PD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,BE平分∠ABC,D是边AB上一点,以BD为直径的⊙O经过点E,且交BC于点F.
(1)求证:AC是⊙O的切线;
(2)若BF=6,⊙O的半径为5,求CE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
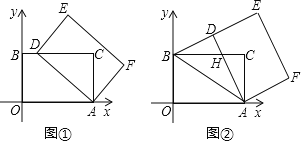
【题目】在平面直角坐标系中,四边形AOBC是矩形,点O(0,0),点A(5,0),点B(0,3).以点A为中心,顺时针旋转矩形AOBC,得到矩形ADEF,点O,B,C的对应点分别为D,E,F.
(1)如图①,当点D落在BC边上时,求点D的坐标;
(2)如图②,当点D落在线段BE上时,AD与BC交于点H.
①求证△ADB≌△AOB;
②求点H的坐标.
(3)记K为矩形AOBC对角线的交点,S为△KDE的面积,求S的取值范围(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
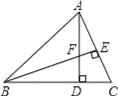
【题目】如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为D,E,AD与BE相交于点F.
(1)求证:△ACD∽△BFD;
(2)当tan∠ABD=1,AC=3时,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的两边长AB=18cm,AD=4cm,点P、Q分别从A、B同时出发,P在边AB上沿AB方向以每秒2cm的速度匀速运动,Q在边BC上沿BC方向以每秒1cm的速度匀速运动.设运动时间为x秒,△PBQ的面积为y(cm2).
(1)求y关于x的函数关系式,并写出x的取值范围;
(2)求△PBQ的面积的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,AB是的直径,PA与⊙O 相切于点A,点C在⊙O 上,且PC=PA,
(1)求证PC是⊙O的切线;
(2)过点C作CD⊥AB于点E,交⊙O于点D,若CD=PA=2![]() ,
,
①求图中阴影部分面积;
②连接AC,若△PAC的内切圆圆心为I,则线段IE的长为 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com