
【题目】如图,平行四边形纸片ABCD的边AB,BC的长分别是10cm和7.5cm,将其四个角向内对折后,点B与点C重合于点C',点A与点D重合于点A′.四条折痕围成一个“信封四边形”EHFG,其顶点分别在平行四边形ABCD的四条边上,则EF=__cm.
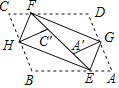
【答案】10.
【解析】
先根据有三个角是直角的四边形是矩形证明四边形EHFG是矩形,再证明△FCH≌△EAG,可得CF=AE=FC',可知EF=AB,即可得结论.
如图中,
由翻折可知:∠CHF=∠FHC',∠BHE=∠EHC',
∴∠FHE=∠FHC'+∠EHC'![]() (∠CHC'+∠BHC')=90°,
(∠CHC'+∠BHC')=90°,
同法可证:∠HFG=∠GEH=90°,
∴四边形EHFG是矩形.
∴FH=EG,FH∥EG,
∴∠HFC'=∠FEG,
∵∠CFH=∠HFC',∠AEG=∠GEA',
∴∠CFH=∠AEG,
∵四边形ABCD是平行四边形,
∴∠C=∠A,BC=AD,
由翻折得:CH=C'H=BH![]() BC,AG=A'G=DG
BC,AG=A'G=DG![]() AD,
AD,
∴CH=AG,
∴△HCF≌△GAE(AAS),
∴CF=AE,
∴EF=FC'+EC'=AE+BE=AB=10cm,
故答案为:10.


科目:初中数学 来源: 题型:
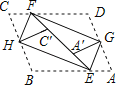
【题目】如图1,AD、BD分别是△ABC的内角∠BAC、∠ABC的平分线,过点A作AE上AD,交BD的延长线于点E.
(1)求证:∠E=![]() ∠C;
∠C;
(2)如图2,如果AE=AB,且BD:DE=2:3,求cos∠ABC的值;
(3)如果∠ABC是锐角,且△ABC与△ADE相似,求∠ABC的度数,并直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
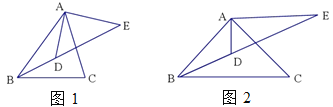
【题目】如图,已知反比例函数y=![]() (x<0)的图象经过OABC的顶点B,点A在x轴上,AC⊥x轴交反比例函数图象于点D,BE⊥x轴于点E,则BE:AD=( )
(x<0)的图象经过OABC的顶点B,点A在x轴上,AC⊥x轴交反比例函数图象于点D,BE⊥x轴于点E,则BE:AD=( )
A. 1:2B. 1:![]() C. 1:3D. 1:
C. 1:3D. 1:![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一种折叠门,由上下轨道和两扇长宽相等的活页门组成,整个活页门的右轴固定在门框
上,通过推动左侧活页门开关;图2是其俯视图简化示意图,已知轨道![]() ,两扇活页门的宽
,两扇活页门的宽![]() ,点
,点![]() 固定,当点
固定,当点![]() 在
在![]() 上左右运动时,
上左右运动时,![]() 与
与![]() 的长度不变(所有结果保留小数点后一位).
的长度不变(所有结果保留小数点后一位).
(1)若![]() ,求
,求![]() 的长;
的长;
(2)当点![]() 从点
从点![]() 向右运动60
向右运动60![]() 时,求点
时,求点![]() 在此过程中运动的路径长.
在此过程中运动的路径长.
(参考数据:sin50°≈0.77, cos50°≈0.64, tan50°≈1.19, π取3.14)

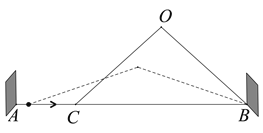
图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】陈老师对他所教的九(1)、九(2)两个班级的学生进行了一次检测,批阅后对最后一道试题的得分情况进行了归类统计(各类别的得分如下表),并绘制了如图所示的每班各类别得分人数的条形统计图(不完整).
各类别的得分表
得分 | 类别 |
|
|
|
|
|
|
|
|
已知两个班一共有![]() 的学生得到两个正确答案,解答完全正确,九(1)班学生这道试题的平均得分为
的学生得到两个正确答案,解答完全正确,九(1)班学生这道试题的平均得分为![]() 分.请解决如下问题:
分.请解决如下问题:
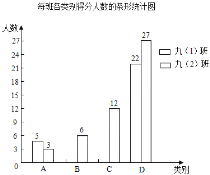
(1)九(2)班学生得分的中位数是 ______;
(2)九(1)班学生中这道试题作答情况属于![]() 类和
类和![]() 类的人数各是多少?
类的人数各是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将在同一平面内如图放置的两块三角板绕公共顶点A旋转,连接BC,DE.探究S△ABC与S△ADC的比是否为定值.
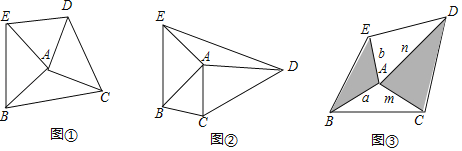
(1)两块三角板是完全相同的等腰直角三角板时,S△ABC:S△ADE是否为定值?如果是,求出此定值,如果不是,说明理由.(图①)
(2)一块是等腰直角三角板,另一块是含有30°角的直角三角板时,S△ABC:S△ADE是否为定值?如果是,求出此定值,如果不是,说明理由.(图②)
(3)两块三角板中,∠BAE+∠CAD=180°,AB=a,AE=b,AC=m,AD=n(a,b,m,n为常数),S△ABC:S△ADE是否为定值?如果是,用含a,b,m,n的式子表示此定值(直接写出结论,不写推理过程),如果不是,说明理由.(图③)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 的顶点为
的顶点为![]() ,与
,与![]() 轴相交于点
轴相交于点![]() ,对称轴为直线
,对称轴为直线![]() ,点
,点![]() 是线段
是线段![]() 的中点.
的中点.
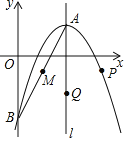
(1)求抛物线的表达式;
(2)写出点![]() 的坐标并求直线
的坐标并求直线![]() 的表达式;
的表达式;
(3)设动点![]() ,
,![]() 分别在抛物线和对称轴l上,当以
分别在抛物线和对称轴l上,当以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边形时,求
为顶点的四边形是平行四边形时,求![]() ,
,![]() 两点的坐标.
两点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为增强学生体质,各学校普遍开展了阳光体育活动,某校为了解全校1000名学生每周课外体育活动时间的情况,随机调查了其中的50名学生,对这50名学生每周课外体育活动时间x(单位:小时)进行了统计.根据所得数据绘制了一幅不完整的统计图,并知道每周课外体育活动时间在6≤x<8小时的学生人数占24%.根据以上信息及统计图解答下列问题:
(1)本次调查属于 调查,样本容量是 ;
(2)请补全频数分布直方图中空缺的部分;
(3)求这50名学生每周课外体育活动时间的平均数;
(4)估计全校学生每周课外体育活动时间不少于6小时的人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
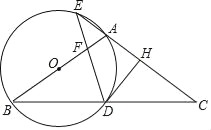
【题目】如图,在△ABC中,AB=AC,以AB为直径作圆O,分别交BC于点D,交CA的延长线于点E,过点D作DH⊥AC于点H,连接DE交线段OA于点F.
(1)求证:DH是圆O的切线;
(2)若A为EH的中点,求![]() 的值;
的值;
(3)若EA=EF=1,求圆O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com