
【题目】(问题原型)
如图①,AB∥CD,点M在直线AB、CD之间,则∠M=∠B+∠D,小明解决上述问题的过程如下:
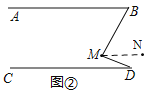
如图②,过点M作MN∥AB
则∠B=_______(_______)
∵AB∥CD,(已知)
MN∥AB(辅助线的做法)
∴MN∥CD(______)
∴∠______=∠D(______)
∴∠B+∠D=∠BMD
请完成小明上面的过程.

(问题迁移)
如图③,AB∥CD,点M与直线CD分别在AB的两侧,猜想∠M、∠B、∠D之间有怎样的数量关系,并加以说明.
(推广应用)
(1)如图④,AB∥CD,点M在直线AB、CD之间,∠ABM的平分线与∠CDM的平分线交于点N,∠M=96°,则∠N=_____°;
(2)如图⑤,AB∥CD,点M与直线CD分别在AB的两侧,∠ABM的平分线与∠CDM的平分线交于点N,∠N=25°,则∠M=______°;
(3)如图⑥,AB∥CD,∠ABG的平分线与∠CDE的平分线交于点M,∠G=78°,∠F=64°,∠E=64°,则∠M=_______°.

【答案】(问题原型)∠BMN;两直线平行,内错角相等;平行于同一条直线的两直线平行;∠NMD;两直线平行,内错角相等;(问题迁移)∠BMD=∠D﹣∠B;证明见解析;(推广应用)(1)∠N=48°;(2)∠M=50°;(3)∠M=39°,
【解析】
(问题原型):过点M作MN∥AB,根据平行线的性质即可得答案;(问题迁移)过点M作MN∥AB,由平行线的性质可得∠1=∠B,∠NMD=∠D,利用角的和差即可得答案;(推广应用):(1)利用图②结论,结合角平分线的性质即可得答案;(2)利用图③的结论,结合角平分线的性质即可得出答案;(3)如图⑥,过G,F,E分别作GN∥AB,FH∥AB,EP∥AB,根据平行线的性质,结合角平分线的性质利用图②的结论即可得出答案.
(问题原型):
如图②,过点M作MN∥AB,
则∠B=∠BMN(两直线平行,内错角相等)
∵AB∥CD,(已知)
∴MN∥AB(辅助线的做法)
∴MN∥CD(平行于同一条直线的两直线平行)
∴∠NMD=∠D(两直线平行,内错角相等)
∴∠B+∠D=∠BMD,
故答案为:∠BMN,两直线平行,内错角相等,平行于同一条直线的两直线平行,∠NMD,两直线平行,内错角相等,
(问题迁移):
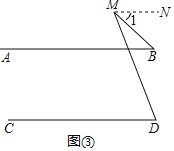
如图③,过点M作MN∥AB,
∴∠1=∠B,
∵AB∥CD,
∴MN∥AB,
∴∠NMD=∠D,
∵∠NMD=∠1+∠BMD,
∴∠BMD=∠D﹣∠B;
(推广应用):
(1)如图④,由如图②的结论可得,∠ABM+∠CDM=∠M=96°,∠N=∠ABN+∠CDN,
∵BN,DN分别平分∠ABM,∠CDM,
∴∠ABN+∠CDN=![]() =
=![]() (∠ABM+∠CDM)=48°,
(∠ABM+∠CDM)=48°,
∴∠N=48°;
(2)如图⑤,由如图③的结论可得,∠M=∠CDM﹣∠ABM,
∵BN,DN分别平分∠ABM,∠CDM,
∴∠CDN﹣∠ABN=![]() ∠CDM﹣
∠CDM﹣![]() ∠ABM=
∠ABM=![]() (∠CDM﹣∠ABM)=
(∠CDM﹣∠ABM)=![]() ∠M=∠N=25°,
∠M=∠N=25°,
∴∠M=50°;
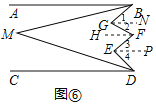
(3)如图⑥,过G,F,E分别作GN∥AB,FH∥AB,EP∥AB,
∵AB∥CD,
∴AB∥GN∥FH∥EP∥CD,
∴∠2=∠GFH,∠3=∠EFH,
∴∠2+∠3=∠GFE=64°,
∴∠1+∠4=∠BGF+∠DEF﹣∠GFE=78°,
∵AB∥GN,EP∥CD,
∴∠ABG=∠1,∠CDE=∠4,
∴∠ABG+∠CDE=78°,
∵BM,DM分别平分∠ABG,∠CDE,
∴∠ABM=![]() ∠ABG,∠CDM=
∠ABG,∠CDM=![]() ∠CDE,
∠CDE,
由如图②中的结论可得∠M=∠ABM+∠CDM=![]() (∠ABG+∠CDE)=
(∠ABG+∠CDE)=![]() ×78°=39°,
×78°=39°,
故答案为:48,50,39.


科目:初中数学 来源: 题型:
【题目】如图,已知AB为⊙O直径,D是 ![]() 的中点,DE⊥AC交AC的延长线于E,⊙O的切线交AD的延长线于F.
的中点,DE⊥AC交AC的延长线于E,⊙O的切线交AD的延长线于F.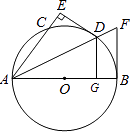
(1)求证:直线DE与⊙O相切;
(2)已知DG⊥AB且DE=4,⊙O的半径为5,求tan∠F的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
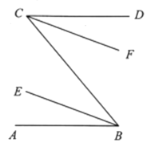
【题目】在下列解题过程的空白处填上适当的内容(推理的理由或数学表达式)如图,已知![]() ,
,![]() 、
、![]() 分别平分
分别平分![]() 和
和![]() ,求证:
,求证:![]() .
.
证明:∵AB//CD,(已知)
∴∠ABC=∠______.(两直线平行,内错角相等)
∵__________.(已知)
∴∠EBC=![]() ∠ABC,(角的平分线定义)
∠ABC,(角的平分线定义)
同理,∠FCB=______.
∵∠EBC=∠FCB.(等量代换)
∴BE//CF.(____________________)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,O是矩形ABCD的对角线的交点,DE∥AC,CE∥BD.
(1)求证:OE⊥DC.
(2)若∠AOD=120°,DE=2,求矩形ABCD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
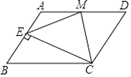
【题目】如图,在平行四边形ABCD中,点M为边AD的中点,过点C作AB的垂线交AB于点E,连接ME,已知AM=2AE=4,∠BCE=30°.
(1)求平行四边形ABCD的面积S;
(2)求证:∠EMC=2∠AEM.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(a,0),B(0,b),实数a、b满足![]() .
.
(1)求点A、点B的坐标;
(2)若点P的坐标是P(-2,x),且![]() ,且△PAB的面积为7,求x的值;
,且△PAB的面积为7,求x的值;
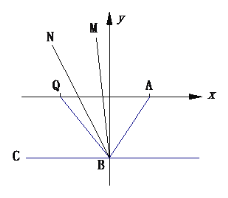
(3)如图,过点B作BC∥x轴,Q是x轴上点A左侧的一动点连接QB,BM平分∠QBA,BN平分∠ABC,当点Q运动时直接写出![]() ____________.
____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学对全校学生进行文明礼仪知识测试,为了解测试结果,随机抽取部分学生的成绩进行分析,将成绩分为三个等级:不合格、一般、优秀,并绘制成如下两幅统计图(不完整).
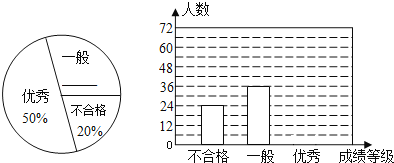
请你根据图中所给的信息解答下列问题:
(1)请将以上两幅统计图补充完整;
(2)若“一般”和“优秀”均被视为达标成绩,则该校被抽取的学生中有______人达标;
(3)若该校学生有学生 2000人,请你估计此次测试中,全校达标的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
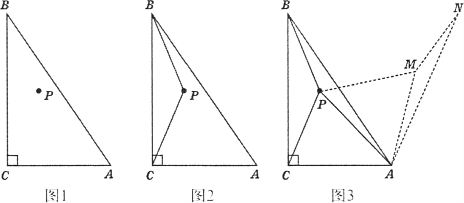
【题目】如图1,在△ABC中,∠ACB=90°,点P为ΔABC内一点.
(1)连接PB,PC,将ABCP沿射线CA方向平移,得到ΔDAE,点B,C,P的对应点分别为点D、A、E,连接CE.
①依题意,请在图2中补全图形;
②如果BP⊥CE,BP=3,AB=6,求CE的长
(2)如图3,以点A为旋转中心,将ΔABP顺时针旋转60°得到△AMN,连接PA、PB、PC,当AC=3,AB=6时,根据此图求PA+PB+PC的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com