
【题目】如图,已知AB为⊙O直径,D是 ![]() 的中点,DE⊥AC交AC的延长线于E,⊙O的切线交AD的延长线于F.
的中点,DE⊥AC交AC的延长线于E,⊙O的切线交AD的延长线于F.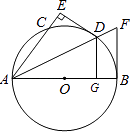
(1)求证:直线DE与⊙O相切;
(2)已知DG⊥AB且DE=4,⊙O的半径为5,求tan∠F的值.
【答案】
(1)证明:连接OD,BC,
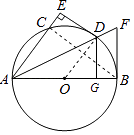
∵D是弧BC的中点,
∴OD垂直平分BC,
∵AB为⊙O的直径,
∴AC⊥BC,
∴OD∥AE.
∵DE⊥AC,
∴OD⊥DE,
∵OD为⊙O的半径,
∴DE是⊙O的切线;
(2)解:∵D是弧BC的中点,
∴ ![]() =
= ![]() ,
,
∴∠EAD=∠BAD,
∵DE⊥AC,DG⊥AB且DE=4,
∴DE=DG=4,
∵DO=5,
∴GO=3,
∴AG=8,
∴tan∠ADG= ![]() =2,
=2,
∵BF是⊙O的切线,
∴∠ABF=90°,
∴DG∥BF,
∴tan∠F=tan∠ADG=2.
【解析】(1)连接BC、OD,由D是弧BC的中点,由垂径定理可得OD⊥BC;再直径所对的圆周角为直角得到BC⊥AC,再证得OD⊥DE,即可得到DE是⊙O的切线;
(2)直接利用勾股定理得出GO的长,再利用切线判定得到BF是⊙O的切线得到DG∥BF,再用锐角三角函数关系得出tan∠F的值.
【考点精析】解答此题的关键在于理解垂径定理的相关知识,掌握垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧,以及对解直角三角形的理解,了解解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法).


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
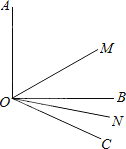
【题目】如图所示,已知∠AOB=90°,∠BOC=20°,OM平分∠AOC,ON平分∠BOC;
(1)求∠MON;
(2)∠AOB=α,∠BOC=β,求∠MON的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知动点P以每秒2㎝的速度沿图甲的边框按从![]() 的路径移动,相应的△ABP的面积S关于时间t的函数图象如图乙.若AB=6,试回答下列问题:
的路径移动,相应的△ABP的面积S关于时间t的函数图象如图乙.若AB=6,试回答下列问题:

(1)图甲中的BC长是多少?
(2)图乙中的a是多少?
(3)图甲中的图形面积的多少?
(4)图乙的b是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一个图形先沿着一条直线进行轴对称变换,再沿着与这条直线平行的方向平移,我们把这样的图形变换叫做滑动对称变换.结合轴对称变换和平移变换的有关性质,你认为在滑动对称变换过程中,这两个对应三角形(如图)的对应点所具有的性质是( ).

A. 对应点所连线段都相等 B. 对应点所连线段被对称轴平分
C. 对应点连线与对称轴垂直 D. 对应点连线互相平行
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为提倡节约用水,准备实行自来水“阶梯计费”方式,用户用水不超出基本用水量的部分享受基本价格,超出基本用水量的部分实行超价收费,为更好地决策,自来水公司的随机抽取了部分用户的用水量数据,并绘制了如图不完整的统计图,(每组数据包括在右端点但不包括左端点),请你根据统计图解答下列问题:
(1)此次抽样调查的样本容量是 .
(2)补全频数分布直方图,求扇形图中“15吨~20吨”部分的圆心角的度数.
(3)如果自来水公司将基本用水量定为每户25吨,那么该地区6万用户中约有多少用户的用水全部享受基本价格?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,D为AB边上任意一点,DF∥AC交BC于F,AE∥BC,∠CDE=∠ABC=∠ACB=α.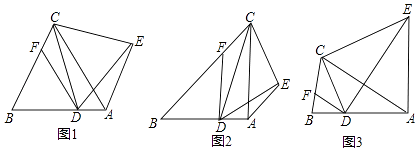
(1)如图1,当α=60°时,求证:△DCE是等边三角形.
(2)如图2.当α=45°时,求证:① ![]() =
= ![]() ;②CE⊥DE.
;②CE⊥DE.
(3)如图3,当α为任意锐角时,请直接写出线段CE与DE的数量关系(用α表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题原型)
如图①,AB∥CD,点M在直线AB、CD之间,则∠M=∠B+∠D,小明解决上述问题的过程如下:
如图②,过点M作MN∥AB
则∠B=_______(_______)
∵AB∥CD,(已知)
MN∥AB(辅助线的做法)
∴MN∥CD(______)
∴∠______=∠D(______)
∴∠B+∠D=∠BMD
请完成小明上面的过程.

(问题迁移)
如图③,AB∥CD,点M与直线CD分别在AB的两侧,猜想∠M、∠B、∠D之间有怎样的数量关系,并加以说明.
(推广应用)
(1)如图④,AB∥CD,点M在直线AB、CD之间,∠ABM的平分线与∠CDM的平分线交于点N,∠M=96°,则∠N=_____°;
(2)如图⑤,AB∥CD,点M与直线CD分别在AB的两侧,∠ABM的平分线与∠CDM的平分线交于点N,∠N=25°,则∠M=______°;
(3)如图⑥,AB∥CD,∠ABG的平分线与∠CDE的平分线交于点M,∠G=78°,∠F=64°,∠E=64°,则∠M=_______°.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com