
【题目】如图所示,沿AE折叠矩形,点D恰好落在BC边上的点F处,已知AB=8cm,BC=10cm,求EC的长.

【答案】3
【解析】
先根据矩形的性质得AD=BC=10,AB=CD=8,再根据折叠的性质得AF=AD=10,EF=DE,在Rt△ABF中,利用勾股定理计算出BF=6,则CF=BCBF=4,设CE=x,则DE=EF=8x,然后在Rt△ECF中根据勾股定理得到x2+42=(8x)2,再解方程即可得到CE的长.
∵四边形ABCD为矩形,
∴AD=BC=10,AB=CD=8,
∵矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上的F处,
∴AF=AD=10,EF=DE,
在Rt△ABF中,∵BF=![]() =6,
=6,
∴CF=BCBF=106=4,
设CE=x,则DE=EF=8x
在Rt△ECF中,∵CE2+FC2=EF2,
∴x2+42=(8x)2,解得x=3,
即CE=3.


科目:初中数学 来源: 题型:
【题目】如图,已知,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA.下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=AE=EC;④AC=2CD.其中正确的有( ) 个.

A. 1 B. 2 C. 3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店进行店庆活动,决定购进甲、乙两种纪念品,若购进甲种纪念品1件,乙种纪念品2件,需要160元;购进甲种纪念品2件,乙种纪念品3件,需要280元.
(1)购进甲乙两种纪念品每件各需要多少元?
(2)该商场决定购进甲乙两种纪念品100件,并且考虑市场需求和资金周转,用于购买这些纪念品的资金不少于6300元,同时又不能超过6430元,则该商场共有几种进货方案?
(3)若销售每件甲种纪念品可获利30元,每件乙种纪念品可获利12元,在第(2)问中的各种进货方案中,哪种方案获利最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,DE⊥AB于E,F在AC上,且BD=DF.
(1)求证:CF=EB;
(2)试判断AB与AF,EB之间存在的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=![]() .其中正确的结论有( )
.其中正确的结论有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在校运会之前想了解九年级女生一分钟仰卧起坐得分情况(满分为7分),在九年级500名女生中随机抽出60名女生进行一次抽样摸底测试所得数据如下表:
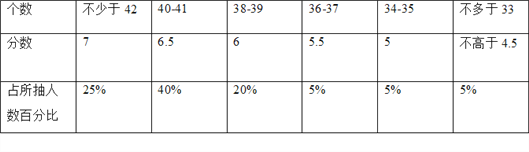
(1)从表中看出所抽的学生所得的分数数据的众数是______.
A.40% B.7 C.6.5 D.5%
(2)请将下面统计图补充完整.
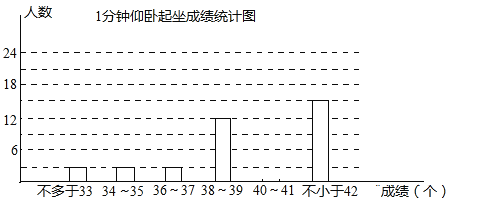
(3)根据上述抽查,请估计该校考试分数不低于6分的人数会有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形OP1A1B1,A1P2A2B2,A2P3A3B3,……,An-1PnAnBn都是正方形,对角线OA1,A1A2,A2A3,……,An-1An都在y轴上(n≥1的整数),点P1(x1,y1),P2(x2,y2),……,Pn(xn,yn)在反比例函数y=![]() (x>0)的图象上,并已知B1(-1,1).
(x>0)的图象上,并已知B1(-1,1).

(1)求反比例函数y=![]() 的解析式;
的解析式;
(2)求点P2和P3的坐标;
(3)由(1)、(2)的结果或规律试猜想并直接写出:△PnBnO的面积为 ,点Pn的坐标为______(用含n的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线y=kx+4(k≠0)与y轴交于点A.
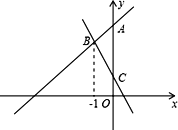
(1)如图,直线y=﹣2x+1与直线y=kx+4(k≠0)交于点B,与y轴交于点C,点B的横坐标为-1.
①求点B的坐标及k的值;
②直线y=﹣2x+1与直线y=kx+4与y轴所围成的△ABC的面积等于 ;
(2)直线y=kx+4(k≠0)与x轴交于点E(x 0 ,0),若﹣2<x 0 <﹣1,求k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com