
【题目】 如图,△ABC中,AB=AC,∠BAC=90°,点D是直线AB上的一动点(不和A、B重合),BE⊥CD于E,交直线AC于F.
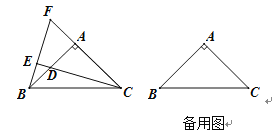
(1)点D在边AB上时,试探究线段BD、AB和AF的数量关系,并证明你的结论;
(2)点D在AB的延长线或反向延长线上时,(1)中的结论是否成立?若不成立,请直接写出正确结论.
【答案】(1)见解析;(2)见解析
【解析】 试题分析:(1)通过三角形全等的判定ASA证明△FAB≌△DAC,然后根据全等三角形的性质可证得结论;
(2)根据题意,分为:点D在AB的延长线上;点D在AB的反向延长线上,两种情况进行讨论即可.
试题解析:(1)如图1,

∵BE⊥CD即∠BEC=90°,∠BAC=90°,
∴∠F+∠FBA=90°,∠F+∠FCE=90°.
∴∠FBA=∠FCE.
∵∠FAB=180°-∠DAC=90°,
∴∠FAB=∠DAC.
在△FAB和△DAC中,
![]()
AB=AC
![]()
∴△FAB≌△DAC(ASA).
∴FA=DA.
∴AB=AD+BD=FA+BD.
(2)(1)中的结论不成立.
点D在AB的延长线上时,AB=AF-BD;点D在AB的反向延长线上时,AB=BD-AF.
理由如下:
①当点D在AB的延长线上时,如图2.
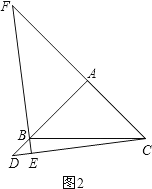
同理可得:FA=DA.
则AB=AD-BD=AF-BD.
②点D在AB的反向延长线上时,如图3.
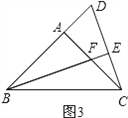
同理可得:FA=DA.
则AB=BD-AD=BD-AF.


 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=1,BC=![]() ,在AC边上截取AD=BC,连接BD.
,在AC边上截取AD=BC,连接BD.
(1)通过计算,判断AD2与ACCD的大小关系;
(2)求∠ABD的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=6cm,BC=8cm,动点P从点C出发,按C→B→A的路径,以2cm每秒的速度运动,设运动时间为t秒,当t为时,△ACP是等腰三角形. 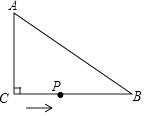
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,两个全等的等边三角形的边长为1m,一个微型机器人由A点开始按ABCDBEA的顺序沿等边三角形的边循环运动,行走2012m停下,则这个微型机器人停在( )

A.点A处 B.点B处 C.点C处 D.点E处
查看答案和解析>>
科目:初中数学 来源: 题型:
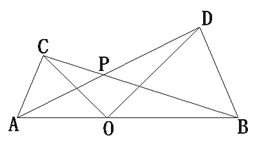
【题目】如图,点O为线段AB上任意一点(不与A、B重合),分别以AO、BO为一腰在AB的同侧作等腰△AOC和等腰△BOD,OA=OC,OB=OD,∠AOC与∠BOD都是锐角,且∠AOC=∠BOD ,AD与BC交于点P.
(1)试说明CB=AD;
(2)若∠COD =80°,求∠APB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场在世界杯足球比赛期间举行促销活动,并设计了两种方案:一种是以商品价格的九五折优惠的方式进行销售;一种是采用有奖销售的方式,具体措施是:①有奖销售自2009年6月9日起,发行奖券10000张,发完为止;②顾客累计购物满400元,赠送奖券一张(假设每位顾客购物每次都恰好凑足400元);③世界杯后,顾客持奖券参加抽奖;④奖项是:特等奖2名,各奖3000元奖品;一等奖10名,各奖1000元奖品;二等奖20名,各奖300元奖品;三等奖100名,各奖100元奖品;四等奖200名,各奖50元奖品;纪念奖5000名,各奖10元奖品,试就商场的收益而言,对两种促销方法进行评价,选用哪一种更为合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
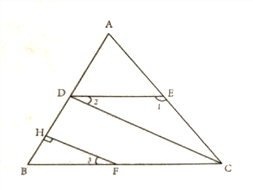
【题目】完成证明并写出推理根据
已知,如图,∠1=132![]() ,∠ACB=48
,∠ACB=48![]() ,∠2=∠3,FH⊥AB于H,
,∠2=∠3,FH⊥AB于H,
求证:CD⊥AB.
证明:∵∠1=132![]() , ∠ACB=48
, ∠ACB=48![]()
∴∠l+∠ACB=180![]()
∴DE∥BC
∴∠2=∠DCB( )
又∵∠2=∠3
∴∠3=∠DCB( )
∴HF∥DC ( )
∴∠CDB=∠FHB. ( )
又∵FH⊥AB,
∴∠FHB=90![]()
∴∠CDB= ![]()
∴CD⊥AB. ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学李老师给学生出了这样一个问题:探究函数y= ![]() 的图象与性质,小斌根据学习函数的经验,对函数y=
的图象与性质,小斌根据学习函数的经验,对函数y= ![]() 的图象与性质进行了探究.下面是小斌的探究过程,请您补充完成:
的图象与性质进行了探究.下面是小斌的探究过程,请您补充完成: 
(1)函数y= ![]() 的自变量x的取值范围是:
的自变量x的取值范围是:
(2)列出y与x的几组对应值,请直接写出m的值,m= .
x | … | ﹣5 | ﹣4 | ﹣3 | ﹣2 | ﹣ | ﹣ | 0 | 1 | 2 | m | 4 | 5 | … |
y | … | | | | 2 | 3 | ﹣1 | 0 | | | | | | … |
(3)请在平面直角坐标系xOy中,描出以上表中各对对应值为坐标的点,并画出该函数的图象;
(4)结合函数的图象,写出函数y= ![]() 的一条性质.
的一条性质.
查看答案和解析>>
科目:初中数学 来源: 题型:
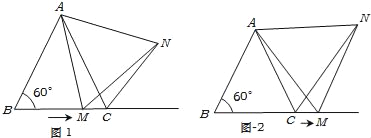
【题目】如图1,在△ABC中,∠B=60°,点M从点B出发沿射线BC方向,在射线BC上运动.在点M运动的过程中,连结AM,并以AM为边在射线BC上方,作等边△AMN,连结CN.
(1)当∠BAM= °时,AB=2BM;
(2)请添加一个条件: ,使得△ABC为等边三角形;
①如图1,当△ABC为等边三角形时,求证:BM=CN;
②如图2,当点M运动到线段BC之外时,其它条件不变,①中结论BM=CN还成立吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com