
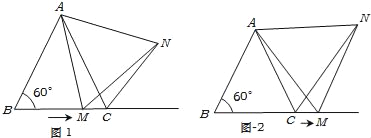
【题目】如图1,在△ABC中,∠B=60°,点M从点B出发沿射线BC方向,在射线BC上运动.在点M运动的过程中,连结AM,并以AM为边在射线BC上方,作等边△AMN,连结CN.
(1)当∠BAM= °时,AB=2BM;
(2)请添加一个条件: ,使得△ABC为等边三角形;
①如图1,当△ABC为等边三角形时,求证:BM=CN;
②如图2,当点M运动到线段BC之外时,其它条件不变,①中结论BM=CN还成立吗?请说明理由.
【答案】(1)30;(2)AB=AC;①见解析;②成立
【解析】试题分析:(1)根据含30°角的直角三角形的性质解答即可;
(2)利用等边三角形的判定解答;
①利用等边三角形的性质和全等三角形的判定证明即可;
②利用等边三角形的性质和全等三角形的判定证明即可.
试题解析:(1)当∠BAM=30°时,
∴∠AMB=180°﹣60°﹣30°=90°,
∴AB=2BM;
故答案为:30;
(2)添加一个条件AB=AC,可得△ABC为等边三角形;
故答案为:AB=AC;
①∵△ABC与△AMN是等边三角形,
∴AB=AC,AM=AN,∠BAC=∠MAN=60°,
∴∠BAC﹣∠MAC=∠MAN﹣∠MAC,
即∠BAM=∠CAN,
在△BAM与△CAN中,
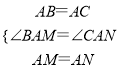 ,
,
∴△BAM≌△CAN(SAS),
∴BM=CN;
②成立,理由如下;
∵△ABC与△AMN是等边三角形,
∴AB=AC,AM=AN,∠BAC=∠MAN=60°,
∴∠BAC+∠MAC=∠MAN+∠MAC,
即∠BAM=∠CAN,
在△BAM与△CAN中,
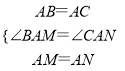 ,
,
∴△BAM≌△CAN(SAS),
∴BM=CN.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:
【题目】 如图,△ABC中,AB=AC,∠BAC=90°,点D是直线AB上的一动点(不和A、B重合),BE⊥CD于E,交直线AC于F.
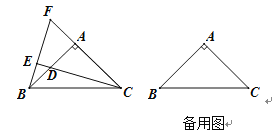
(1)点D在边AB上时,试探究线段BD、AB和AF的数量关系,并证明你的结论;
(2)点D在AB的延长线或反向延长线上时,(1)中的结论是否成立?若不成立,请直接写出正确结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某职业高中机电班共有学生42人,其中男生人数比女生人数的2倍少3人.
(1)该班男生和女生各有多少人?
(2)某工厂决定到该班招录30名学生,经测试,该班男、女生每天能加工的零件数分别为50个和45个,为保证他们每天加工的零件总数不少于1460个,那么至少要招录多少名男学生?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暑假期间,学校布置了综合实践活动任务,王涛小组四人负责调查本村的500户农民的家庭收入情况,他们随机调查了40户居民家庭的收入情况(收入取整数,单位:元),并制定了频数分布表(如图Ⅰ)和频数分布直方图(如图Ⅱ).


根据以上提供的信息,解答下列问题:
(1)补全频数分布表;
(2)补全频数分布直方图;
(3)请你估计该村属于中等收入(不低于1000元小于1600元)的大约有多少户?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=8,BC=15,点E是AD边上一点,连接BE,把△ABE沿BE折叠,使点A落在点A′处,点F是CD边上一点,连接EF,把△DEF沿EF折叠,使点D落在直线EA′上的点D′处,当点D′落在BC边上时,AE的长为 . 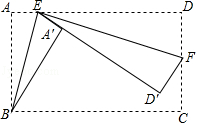
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果店以4元/千克的价格购进一批水果,由于销售状况良好,该店又再次购进同一种水果,第二次进货价格比第一次每千克便宜了0.5元,所购水果重量恰好是第一次购进水果重量的2倍,这样该水果店两次购进水果共花去了2200元.
(1)该水果店两次分别购买了多少元的水果?
(2)在销售中,尽管两次进货的价格不同,但水果店仍以相同的价格售出,若第一次购进的水果有3%的损耗,第二次购进的水果有5%的损耗,该水果店希望售完这些水果获利不低于1244元,则该水果每千克售价至少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
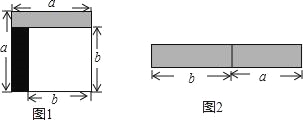
【题目】从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
(1)上述操作能验证的等式是 ;(请选择正确的一个)
A、a2﹣2ab+b2=(a﹣b)2
B、a2﹣b2=(a+b)(a﹣b)
C、a2+ab=a(a+b)
(2)应用你从(1)选出的等式,完成下列各题:
①已知x2﹣4y2=12,x+2y=4,求x﹣2y的值.
②计算:(1﹣![]() )(1﹣
)(1﹣![]() )(1﹣
)(1﹣![]() )…(1﹣
)…(1﹣![]() )(1﹣
)(1﹣![]() ).
).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
(1)上述操作能验证的等式是 ;(请选择正确的一个)
A、a2﹣2ab+b2=(a﹣b)2
B、a2﹣b2=(a+b)(a﹣b)
C、a2+ab=a(a+b)
(2)应用你从(1)选出的等式,完成下列各题:
①已知x2﹣4y2=12,x+2y=4,求x﹣2y的值.
②计算:(1﹣![]() )(1﹣
)(1﹣![]() )(1﹣
)(1﹣![]() )…(1﹣
)…(1﹣![]() )(1﹣
)(1﹣![]() ).
).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图△ABC中,∠A=96°,延长BC到D,∠ABC与∠ACD的平分线相交于点A1∠A1BC与∠A1CD的平分线相交于点A2,依此类推,∠A4BC与∠A4CD的平分线相交于点A5,则∠A5的度数为( )

A. 19.2° B. 8° C. 6° D. 3°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com