
【题目】如图,矩形ABCD中,AB=8,BC=15,点E是AD边上一点,连接BE,把△ABE沿BE折叠,使点A落在点A′处,点F是CD边上一点,连接EF,把△DEF沿EF折叠,使点D落在直线EA′上的点D′处,当点D′落在BC边上时,AE的长为 . 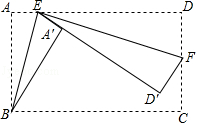
【答案】![]() 或
或 ![]()
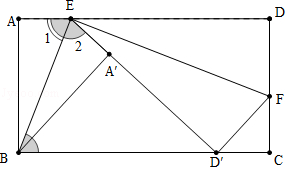
【解析】解:∵把△ABE沿BE折叠,使点A落在点A′处, ∴AE=AE′,AB=BE′=8,∠A=∠BE′E=90°,
∵把△DEF沿EF折叠,使点D落在直线EA′上的点D′处,
∴DE=D′E,DF=D′F,∠ED′F=∠D=90°,
设AE=A′E=x,则DE=ED′=15﹣x,
∵AD∥BC,
∴∠1=∠EBC,
∵∠1=∠2,
∴∠2=∠EBD′,
∴BD′=ED′=15﹣x,
∴A′D′=15﹣2x,
在Rt△BA′D′中,
∵BD′2=BA′2+A′D′2 ,
∴82+(15﹣2x)2=(15﹣x)2 ,
解得x= ![]() ,
,
∴AE= ![]() 或
或 ![]() .
.
【考点精析】关于本题考查的矩形的性质和翻折变换(折叠问题),需要了解矩形的四个角都是直角,矩形的对角线相等;折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等才能得出正确答案.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
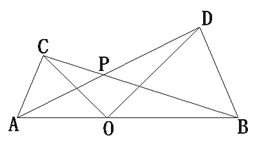
【题目】如图,点O为线段AB上任意一点(不与A、B重合),分别以AO、BO为一腰在AB的同侧作等腰△AOC和等腰△BOD,OA=OC,OB=OD,∠AOC与∠BOD都是锐角,且∠AOC=∠BOD ,AD与BC交于点P.
(1)试说明CB=AD;
(2)若∠COD =80°,求∠APB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富同学们的课余生活,某学校举行“亲近大自然”户外活动,现随机抽取了部分学生进行主题为“你最想去的景点是?”的问卷调查,要求学生只能从“A(植物园),B(花卉园),C(湿地公园),D(森林公园)”四个景点中选择一项,根据调查结果,绘制了如下两幅不完整的统计图. 
请解答下列问题:
(1)本次调查的样本容量是;
(2)补全条形统计图;
(3)若该学校共有3600名学生,试估计该校最想去湿地公园的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】应用题
有A、B两个商场以同样价格出售同样商品,且各自推出了不同的优惠方案:
在A商场累计购物超过200元后,超出部分按80%收费;
在B商场累计购物满100元后,超出的部分按90%收费。
设累计购物x(x>200)元,用x表示A、B两商场的实际费用并指明顾客选择到哪家购物合适?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】推理填空:如图AB∥CD,∠1=∠2,∠3=∠4,试说明AD∥BE.
解:∵AB∥CD(已知)
∴∠4=∠1+_____(_______)
∵∠3=∠4(已知)
∴∠3=∠1+_____(_______)
∵∠1=∠2(已知)
∴∠1+∠CAF=∠2+∠CAF(_______)
即∠_____=∠_____
∴∠3=∠_____(_______)
∴AD∥BE(_______).

查看答案和解析>>
科目:初中数学 来源: 题型:
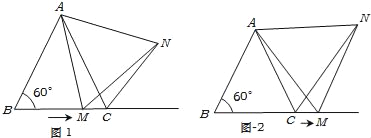
【题目】如图1,在△ABC中,∠B=60°,点M从点B出发沿射线BC方向,在射线BC上运动.在点M运动的过程中,连结AM,并以AM为边在射线BC上方,作等边△AMN,连结CN.
(1)当∠BAM= °时,AB=2BM;
(2)请添加一个条件: ,使得△ABC为等边三角形;
①如图1,当△ABC为等边三角形时,求证:BM=CN;
②如图2,当点M运动到线段BC之外时,其它条件不变,①中结论BM=CN还成立吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,BD平分∠ABC,CD平分∠ACB,过点D作EF∥BC,与AB、AC分别相交于E、F,若已知AB=9,AC=7,求△AEF的周长.
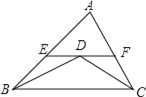
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,点E在边BC上,如果点F是边AD上的点,那么△CDF与△ABE不一定全等的条件是( )
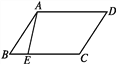
A. DF=BE B. AF=CE
C. CF=AE D. CF∥AE
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com