
【题目】完成证明并写出推理根据
已知,如图,∠1=132![]() ,∠ACB=48
,∠ACB=48![]() ,∠2=∠3,FH⊥AB于H,
,∠2=∠3,FH⊥AB于H,
求证:CD⊥AB.
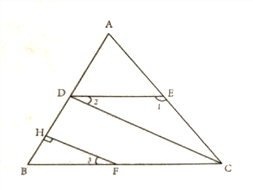
证明:∵∠1=132![]() , ∠ACB=48
, ∠ACB=48![]()
∴∠l+∠ACB=180![]()
∴DE∥BC
∴∠2=∠DCB( )
又∵∠2=∠3
∴∠3=∠DCB( )
∴HF∥DC ( )
∴∠CDB=∠FHB. ( )
又∵FH⊥AB,
∴∠FHB=90![]()
∴∠CDB= ![]()
∴CD⊥AB. ( )
【答案】详见解析
【解析】求出∠1+∠ACB=180°,根据平行线的判定得出DE∥BC,根据平行线的性质得出∠2=∠DCB,求出∠3=∠DCB,根据平行线的判定得出HF∥CD,根据平行线的性质得出∠CDB=∠FHB,即可求出答案.
∵∠1=132o,∠ACB=48o,
∴∠1+∠ACB=180°.
∴DE∥BC.
∴∠2=∠DCB(两直线平行,内错角相等) .
又∵∠2=∠3.
∴∠3=∠DCB(等量代换).
∴HF∥DC(同位角相等,两直线平行) .
∴∠CDB=∠FHB. (两直线平行,同位角相等) .
又∵FH⊥AB,
∴∠FHB=90°(垂直定义).
∴∠CDB=90°.
∴CD⊥AB. (垂直的定义) .


科目:初中数学 来源: 题型:
【题目】已知一次函数y1=kx+b的图像经过点(0,-2),(2,2).
(1)求一次函数的表达式,并在所给直角坐标系中画出此函数的图像;;
(2)根据图像回答:当x 时,y1=0;
(3)求直线y1=kx+b、直线y2=-2x+4与y轴围成的三角形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以∠AOB的顶点O为圆心,适当长为半径画弧,交OA于点C,交OB于点D.再分别以点C、D为圆心,大于![]() CD的长为半径画弧,两弧在∠AOB内部交于点E,过点E作射线OE,连接CD.则下列说法错误的是
CD的长为半径画弧,两弧在∠AOB内部交于点E,过点E作射线OE,连接CD.则下列说法错误的是

A.射线OE是∠AOB的平分线
B.△COD是等腰三角形
C.C、D两点关于OE所在直线对称
D.O、E两点关于CD所在直线对称
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,△ABC中,AB=AC,∠BAC=90°,点D是直线AB上的一动点(不和A、B重合),BE⊥CD于E,交直线AC于F.
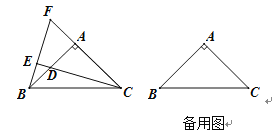
(1)点D在边AB上时,试探究线段BD、AB和AF的数量关系,并证明你的结论;
(2)点D在AB的延长线或反向延长线上时,(1)中的结论是否成立?若不成立,请直接写出正确结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形OABC中,已知点A、C两点的坐标为A (![]() ,
,![]() ),C (2
),C (2![]() ,0).
,0).
(1)求点B的坐标.
(2)将平行四边形OABC向左平移![]() 个单位长度,求所得四边形A′B′C′O′四个顶点的坐标.
个单位长度,求所得四边形A′B′C′O′四个顶点的坐标.
(3)求平行四边形OABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,AB=AC,点D是BC的中点,点E在AD上,连接BE、CE.
(1)求证:BE=CE
(2)如图2,若BE的延长线交AC于点F,且BF ⊥AC,垂足为F,原题设其它条件不变.求证:∠CAD=∠CBF
(3)在(2)的条件下,若∠BAC=45![]() ,判断△CFE的形状,并说明理由.
,判断△CFE的形状,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一楼房AB后有一假山,其坡度为i=1: ![]() ,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高.(注:坡度i是指坡面的铅直高度与水平宽度的比)
,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=25米,与亭子距离CE=20米,小丽从楼房顶测得E点的俯角为45°,求楼房AB的高.(注:坡度i是指坡面的铅直高度与水平宽度的比)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某职业高中机电班共有学生42人,其中男生人数比女生人数的2倍少3人.
(1)该班男生和女生各有多少人?
(2)某工厂决定到该班招录30名学生,经测试,该班男、女生每天能加工的零件数分别为50个和45个,为保证他们每天加工的零件总数不少于1460个,那么至少要招录多少名男学生?
查看答案和解析>>
科目:初中数学 来源: 题型:
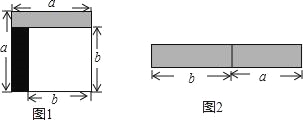
【题目】从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).
(1)上述操作能验证的等式是 ;(请选择正确的一个)
A、a2﹣2ab+b2=(a﹣b)2
B、a2﹣b2=(a+b)(a﹣b)
C、a2+ab=a(a+b)
(2)应用你从(1)选出的等式,完成下列各题:
①已知x2﹣4y2=12,x+2y=4,求x﹣2y的值.
②计算:(1﹣![]() )(1﹣
)(1﹣![]() )(1﹣
)(1﹣![]() )…(1﹣
)…(1﹣![]() )(1﹣
)(1﹣![]() ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com