
【题目】如图,平行四边形ABCD的对角线AC、BD相交于点O,EF过点O且与AB、CD分别相交于点E、F,连接EC.
(1)求证:OE=OF;
(2)若EF⊥AC,平行四边形ABCD的周长是22,求△BEC的周长.
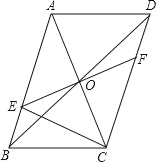
【答案】(1)见解析;(2)11.
【解析】
(1)由已知条件证△DFO≌△BEO即可得到结论;
(2)由平行四边形ABCD的周长为22可得AB+BC=11;由已知易得点O是AC的中点,结合EF⊥AC可得EF是AC的垂直平分线,由此可得AE=EC,从而可得△BEC的周长=BC+BE+EC=BC+BE+AE=BC+AB=11.
(1)∵四边形ABCD是平行四边形,
∴OD=OB,DC∥AB,
∴∠FDO=∠EBO,
在△DFO和△BEO中,
∠FDO=∠EBO,OD=OB,∠FOD=∠EOB,
∴△DFO≌△BEO(ASA),
∴OE=OF.
(2)∵四边形ABCD是平行四边形,
∴AB=CD,AD=BC,OA=OC.
∵EF⊥AC,
∴AE=CE.
∵平行四边形ABCD的周长是22,即2(BC+AB)=22.
∴BC+AB=11,
∴△BEC的周长=BC+BE+CE=BC+BE+AE=BC+AB=11.


科目:初中数学 来源: 题型:
【题目】如图,直线y=k1x(x≥0)与双曲线y=![]() (x>0)相交于点P(2,4).已知点A(4,0),B(0,3),连接AB,将Rt△AOB沿OP方向平移,使点O移动到点P,得到△A′PB′.过点A′作A′C∥y轴交双曲线于点C,连接CP.
(x>0)相交于点P(2,4).已知点A(4,0),B(0,3),连接AB,将Rt△AOB沿OP方向平移,使点O移动到点P,得到△A′PB′.过点A′作A′C∥y轴交双曲线于点C,连接CP.
(1)求k1与k2的值;
(2)求直线PC的解析式;
(3)直接写出线段AB扫过的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某校为了创建书香校园,去年购进一批图书.经了解,科普书的单价比文学书的单价多4元,用12000元购进的科普书与用8000元购进的文学书本数相等.
(1)文学书和科普书的单价各多少钱?
(2)今年文学书和科普书的单价和去年相比保持不变,该校打算用10000元再购进一批文学书和科普书,问购进文学书550本后至多还能购进多少本科普书?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】密苏里州圣路易斯拱门是座雄伟壮观的抛物线形的建筑物,是美国最高的独自挺立的纪念碑,如图.拱门的地面宽度为200米,两侧距地面高150米处各有一个观光窗,两窗的水平距离为100米,求拱门的最大高度. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,定义点P(x,y)的变换点为P′(x+y,x﹣y).
(1)如图1,如果⊙O的半径为2 ![]() ,
,
①请你判断M(2,0),N(﹣2,﹣1)两个点的变换点与⊙O的位置关系;
②若点P在直线y=x+2上,点P的变换点P′在⊙O的内,求点P横坐标的取值范围.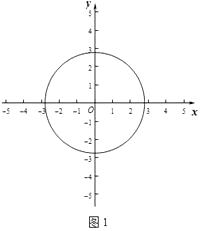
(2)如图2,如果⊙O的半径为1,且P的变换点P′在直线y=﹣2x+6上,求点P与⊙O上任意一点距离的最小值. 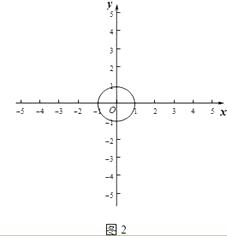
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠ADB=∠ADC,则不一定能使△ABD≌△ACD的条件是( )

A. AB=AC B. BD=CD C. ∠B=∠C D. ∠BAD=∠CAD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】射线QN与等边△ABC的两边AB,BC分别交于点M,N,且AC∥QN,AM=MB=2cm,QM=4cm.动点P从点Q出发,沿射线QN以每秒1cm的速度向右移动,经过t秒,以点P为圆心, ![]() cm为半径的圆与△ABC的边相切(切点在边上),请写出t可取的一切值(单位:秒)
cm为半径的圆与△ABC的边相切(切点在边上),请写出t可取的一切值(单位:秒) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一只甲虫在5![]() 5的方格(每一格边长为1)上沿着网格线运动,从A处出发去看望B、C、D处的甲虫,规定:向上向右为正,向下向左为负.例如:从A到B记为:
5的方格(每一格边长为1)上沿着网格线运动,从A处出发去看望B、C、D处的甲虫,规定:向上向右为正,向下向左为负.例如:从A到B记为:![]() (+1,+3);从C到D 记为:
(+1,+3);从C到D 记为:![]() (+1,-2),其中第一个数表示左右方向,第二个数表示上下方向.
(+1,-2),其中第一个数表示左右方向,第二个数表示上下方向.
(1)填空:![]() 记为( , ),
记为( , ), ![]() 记为( , );
记为( , );
(2)若甲虫的行走路线为:![]() ,请你计算甲虫走过的路程.
,请你计算甲虫走过的路程.
(3)若这只甲虫去Q的行走路线依次为:A→M(+2,+2),M→N(+2,-1),N→P(-2,+3),P→Q(-1,-2),请依次在图2标出点M、N、P、Q的位置.
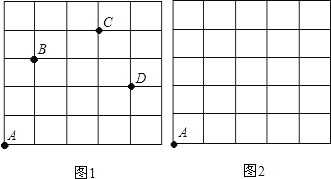
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com