
分析 分两种情况进行讨论:①当点C在y轴上时,如图1,此时△ABC的面积是以AC为底,以点B的横坐标为高;②当点C在x轴上时,如图2,此时△ABC的面积是以AB为底边,以点C到直线AB的距离为高;根据三角形的面积公式,即可解答.
解答 解:①当点C在y轴上时,如图1,此时△ABC的面积是以AC为底,以点B的横坐标为高,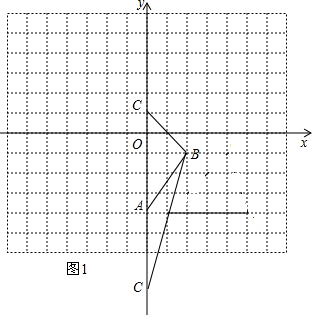
设点C的坐标为(0,y),则AC=|-4-y|,
∴${S}_{△ABC}=\frac{1}{2}×|-4-y|×2$=5,
∴|-4-y|=5,
解得:y=1或y=-9,
∴点C的坐标为(0,1)或(0,-9);
②当点C在x轴上时,如图2,此时△ABC的面积是以AB为底边,以点C到直线AB的距离为高,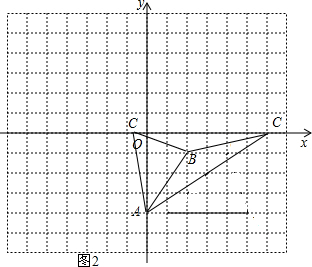
设直线AB的解析式为y=kx+b,
把A(0,-4),点B(2,-1)代入得:$\left\{\begin{array}{l}{b=-4}\\{2k+b=-1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{3}{2}}\\{b=-4}\end{array}\right.$,
∴y=$\frac{3}{2}$x-4,
设点C的坐标为(m,0),
则点C到直线AB的距离为:$\frac{|\frac{3}{2}x-4|}{\sqrt{(\frac{3}{2})^{2}+(-1)^{2}}}=\frac{|3x-8|}{\sqrt{13}}$,
AB=$\sqrt{(-4+1)^{2}+{2}^{2}}=\sqrt{13}$,
∴${S}_{△ABC}=\frac{1}{2}×\sqrt{13}×\frac{|3x-8|}{\sqrt{13}}=5$,
整理得:|3x-8|=10,
解得:x=6或x=-$\frac{2}{3}$,
∴点C的坐标为(6,0)或($-\frac{2}{3}$,0)
综合①②,点C的坐标为(6,0)或($-\frac{2}{3}$,0)或(0,1)或(0,-9).
点评 本题考查图形与坐标,解决本题的关键是分两种情况作出图形,结合三角形面积公式解答.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{3\sqrt{10}}{10}$ | B. | $\frac{\sqrt{10}}{10}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
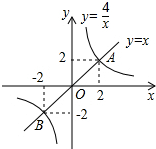 正比例函数y=x与反比例函数y=$\frac{4}{x}$的图象交于A(2,2)、B(-2,-2)两点,当x>$\frac{4}{x}$时,x的取值范围是( )
正比例函数y=x与反比例函数y=$\frac{4}{x}$的图象交于A(2,2)、B(-2,-2)两点,当x>$\frac{4}{x}$时,x的取值范围是( )| A. | -2<x<0或x>2 | B. | -2<x<0或0<x<2 | C. | x>2 | D. | x<-2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
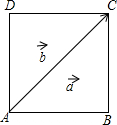 如图,在正方形ABCD中,如果AC=3$\sqrt{2}$,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,那么|$\overrightarrow{a}$-$\overrightarrow{b}$|=3.
如图,在正方形ABCD中,如果AC=3$\sqrt{2}$,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,那么|$\overrightarrow{a}$-$\overrightarrow{b}$|=3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
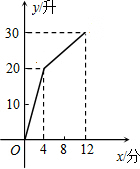 有一进水管与出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,每分的进水量和出水量是两个常数,容器内的水量y(单位:L)与时间x(单位:分)之间的关系如图所示:
有一进水管与出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,每分的进水量和出水量是两个常数,容器内的水量y(单位:L)与时间x(单位:分)之间的关系如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com