
如图1,在平面直角坐标系中,O为坐标原点,P是反比例函数 图象上任意一点,以P为圆心,PO为半径的圆与坐标轴分别交于点A、B.(本小题满分10分)
图象上任意一点,以P为圆心,PO为半径的圆与坐标轴分别交于点A、B.(本小题满分10分)

(1)求证:线段AB为⊙P的直径;
(2)求△AOB的面积;
(3)如图2,Q是反比例函数 图象上异于点P的另一点,以Q为圆心,QO为半径画圆与坐标轴分别交于点C、D,求证:DO·OC=BO·OA.
图象上异于点P的另一点,以Q为圆心,QO为半径画圆与坐标轴分别交于点C、D,求证:DO·OC=BO·OA.
(1)证明见试题解析;(2)24;(3)证明见试题解析.
【解析】
试题分析:(1)∠AOB=90°,由圆周角定理的推论,可以证明AB是⊙P的直径;
(2)将△AOB的面积用含点P坐标的表达式表示出来,容易计算出结果;
(3)对于反比例函数上另外一点Q,⊙Q与坐标轴所形成的△COD的面积,依然不变,与△AOB的面积相等.
解答:(1)证明:∵∠AOB=90°,且∠AOB是⊙P中弦AB所对的圆周角,∴AB是⊙P的直径.
(2)【解析】
设点P坐标为(m,n)(m>0,n>0),
∵点P是反比例函数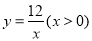 图象上一点,∴mn=12.
图象上一点,∴mn=12.
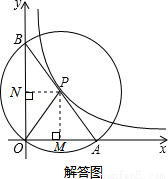
如答图,过点P作PM⊥x轴于点M,PN⊥y轴于点N,则OM=m,ON=n.
由垂径定理可知,点M为OA中点,点N为OB中点,
∴OA=2OM=2m,OB=2ON=2n,
∴S△AOB=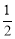 BO•OA=
BO•OA=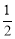 ×2n×2m=2mn=2×12=24.
×2n×2m=2mn=2×12=24.
(3)证明:∵以Q为圆心,QO为半径画圆与坐标轴分别交于点C、D,∠COD=90°,
∴DC是⊙Q的直径.
若点Q为反比例函数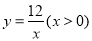 图象上异于点P的另一点,
图象上异于点P的另一点,
参照(2),同理可得:S△COD=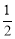 DO•CO=24,
DO•CO=24,
则有:S△COD=S△AOB=24,即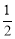 BO•OA=
BO•OA=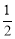 DO•CO,
DO•CO,
∴DO•OC=BO•OA.
考点:反比例函数综合题.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源:2014-2015学年浙江省联盟八年级上学期期中数学试卷(解析版) 题型:解答题
Rt△ABC中,AB=AC=2,∠A=90°,D为BC中点,点E,F分别在AB,AC上,且BE=AF,

(1)求证:ED=FD,
(2)求证:DF⊥DE,
(3)求四边形AFDE的面积.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省杭州地区八年级上学期期中质量检测数学试卷(解析版) 题型:解答题
(本题10分)如图,在△ABC中,AB=AC,AD是BC边上的高,AM是△ABC外角∠CAE的平分线.

(1)用尺规作图方法,作∠ADC的平分线DN;(保留作图痕迹,不写作法和证明)
(2)设DN与AM交于点F,判断△ADF的形状,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省杭州市联盟学校九年级上学期期中考试数学试卷(解析版) 题型:选择题
2014年“十·一”期间,小明与小亮两家准备从农夫乐园、双溪漂流、 超山赏梅选择一景点游玩,小明与小亮通过抽签方式确定景点,则两家抽到同一景点的概率是( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省杭州市联盟学校九年级上学期期中考试数学试卷(解析版) 题型:解答题
如图,在破残的圆形残片上,弦AB的垂直平分线交弧AB于点C,交弦AB于点D,已知AB=8cm,CD=2cm.(本小题满分8分)

(1)求作此残片所在的圆(尺规作图,不写作法,保留作图痕迹);
(2)求出(1)中所作圆的半径.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省杭州市萧山区高桥教育九年级上学期第二次检测数学试卷(解析版) 题型:选择题
若二次函数y=Ax2+C,当x取x1,x2(x1≠x2)时函数值相等,则当x取x1+x2时,函数值为( )
A.A+C B.A-C C.-C D..C
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省杭州市萧山区高桥教育九年级上学期第二次检测数学试卷(解析版) 题型:解答题
(本小题满分6分)分别根据配方法和顶点坐标公式确定下列二次函数的顶点坐标。
 (配方法)
(配方法)
② (公式法)
(公式法)
查看答案和解析>>
科目:初中数学 来源:2014-2015学年浙江省杭州市萧山地区九年级上学期期中考试数学试卷(解析版) 题型:填空题
命题“在同圆或等圆中,若两个圆周角相等,则它们所对的弦也相等”则它的逆命题是 命题(填“真”或“假”)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com