
��ͼ����ƽ��ֱ������ϵ�У�ֱ��y=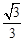 x+1�ֱ����������ύ��B��A���㣬CΪ��ֱ���ϵ�һ���㣬��ÿ��1����λ���ȵ��ٶȴӵ�A��ʼ��ֱ��BA�����ƶ������ȱߡ�CDE����D�͵�E����x���ϣ��Ե�CΪ�����������y=a��x��m��2+n������E����M��x�ᡢֱ��AB�����У���뾶Ϊ3��1��
x+1�ֱ����������ύ��B��A���㣬CΪ��ֱ���ϵ�һ���㣬��ÿ��1����λ���ȵ��ٶȴӵ�A��ʼ��ֱ��BA�����ƶ������ȱߡ�CDE����D�͵�E����x���ϣ��Ե�CΪ�����������y=a��x��m��2+n������E����M��x�ᡢֱ��AB�����У���뾶Ϊ3��1��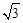 ��a��
��a��
��1�����A������͡�ABO�Ķ�����
��2������C���A�غ�ʱ����a��ֵ��
��3����C�ƶ�������ʱ���ȱߡ�CDE�ı�CE��һ�����M���У�

��1��A�������ǣ�0��1����ABO=30�㣨2����3��3��4��
���������⣺��1����x=0ʱ��y=1����y=0ʱ��x=�� ��
��
��OA=1��OB= ����A�������ǣ�0��1����
����A�������ǣ�0��1����
��tan��ABO=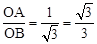 �����ABO=30�㡣
�����ABO=30�㡣
��2���ߡ�CDEΪ�ȱ������Σ���A��0��1������tan30��=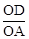 ����OD=
����OD=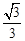 ��
��
��D�������ǣ���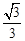 ��0����E�������ǣ�
��0����E�������ǣ�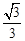 ��0����
��0����
�ѵ�A��0��1����D����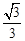 ��0����E��
��0����E��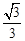 ��0������ y=a��x��m��2+n����
��0������ y=a��x��m��2+n����
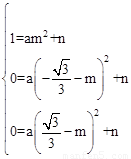 �����
�����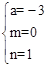 ����a=��3��
����a=��3��
��3����ͼ�����е�ֱ���Q��N��P������MQ��MN��MP��ME������C��CH��x�ᣬHΪ���㣬��A��AF��CH��FΪ���㡣
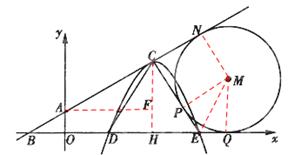
�ߡ�CDE�ǵȱ������Σ���ABO=30�㣬
���BCE=90�㣬��ECN=90�㡣
��CE��AB�ֱ����M���У����MPC=��CNM=90�㡣���ı���MPCNΪ���Ρ�
��MP=MN�����ı���MPCNΪ�����Ρ�
��MP=MN=CP=CN=3��1�� ��a��a��0����
��a��a��0����
��EC��x�ᶼ���M���У���EP=EQ��
�ߡ�NBQ+��NMQ=180�㣬���PMQ=60�㡣���EMQ��=30�㡣
����Rt��MEP��tan30��=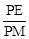 ����PE=��
����PE=�� ��3��a��
��3��a��
��CE=CP+PE=3��1�� ��a+��
��a+�� ��3��a=��2
��3��a=��2 a��
a��
��DH=HE=�� a��CH=��3a��BH=��3
a��CH=��3a��BH=��3 a��
a��
��OH=��3 a��
a�� ��OE=��4
��OE=��4 a��
a�� ��
��
��E����4 a��
a�� ��0����C����3
��0����C����3 a��
a�� ����3a����
����3a����
����κ����Ľ���ʽΪ��y=a��x+3 a+
a+ ��2��3a��
��2��3a��
��E�ڸ��������ϣ���a����4 a��
a�� +3
+3 a+
a+ ��2��3a=0��
��2��3a=0��
�ã�a2=1����֮��a1=1��a2=��1��
��a��0����a=��1��
��AF=2 ��CF=2����AC=4��
��CF=2����AC=4��
���C�ƶ���4��ʱ���ȱߡ�CDE�ı�CE��һ�����M���С�
��1����ֱ֪��AB�Ľ���ʽ�������ʽ��x=0���ܵõ�A�����ꣻ��y=0���ܵõ�B�����ꣻ��Rt��OAB�У�֪��OA��OB�ij��������к������ɵõ���ABO��ֵ��
��2����C��A�غ�ʱ����֪��C�����꣬Ȼ����OC�ij��Լ��ȱ������ε��������OD��OE�ij������ɵõ�D��E�����꣬���ô���ϵ������ȷ��a��ֵ��
��3��������һ������ʱ��ʾ��ͼ����֪������ֻ��Բ�İ뾶����ô����Բ���������е��Լ���E���������жϳ��ı���CPMN�������Σ���ôCP���M�İ뾶��ȣ�ֻҪ�����PE���ܽ�һ�����C�����ꣻ��ô���Դ�PE=EQ����Rt��MEP���֣����ȡ�CED=60�㣬����MEP=��MEQ��������������ǵĶ�����ͨ����ֱ�������β��ѵõ�PE�ij����������PE����C��E�����꣮Ȼ������C��E������ȷ��a��ֵ���Ӷ������AC�ij����ɴ˵ý�


 ��Ȥ������ҵ���ϿƼ�������ϵ�д�
��Ȥ������ҵ���ϿƼ�������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ����ƽ��ֱ�������У��ı���OABC�ǵ������Σ�CB��OA��OA=7��AB=4����COA=60�㣬��PΪx���ϵ�һ�����㣬���ǵ�P�����0����A�غϣ�����CP��D�����߶�AB��һ�㣬����PD��
��ͼ����ƽ��ֱ�������У��ı���OABC�ǵ������Σ�CB��OA��OA=7��AB=4����COA=60�㣬��PΪx���ϵ�һ�����㣬���ǵ�P�����0����A�غϣ�����CP��D�����߶�AB��һ�㣬����PD��| BD |
| AB |
| 5 |
| 8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��2012•�山��һģ����ͼ����ƽ��ֱ������xoy�У�������ԭ��OΪԲ�ģ�3Ϊ�뾶��Բ���Ӵ�Բ�ڣ������߽磩�����������㣨�ᡢ�������Ϊ������������ѡȡһ���㣬��ᡢ������֮��Ϊ0�ĸ�����
��2012•�山��һģ����ͼ����ƽ��ֱ������xoy�У�������ԭ��OΪԲ�ģ�3Ϊ�뾶��Բ���Ӵ�Բ�ڣ������߽磩�����������㣨�ᡢ�������Ϊ������������ѡȡһ���㣬��ᡢ������֮��Ϊ0�ĸ�����| 5 |
| 29 |
| 5 |
| 29 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ����ƽ��ֱ�������У���������ABCD���µ���x���ϣ���B������Ϊ��4��0����D������Ϊ��0��3������AC��Ϊ
��ͼ����ƽ��ֱ�������У���������ABCD���µ���x���ϣ���B������Ϊ��4��0����D������Ϊ��0��3������AC��Ϊ�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��ͼ����ƽ��ֱ������xOy�У���֪��A��-5��0����P�Ƿ���������y=
��ͼ����ƽ��ֱ������xOy�У���֪��A��-5��0����P�Ƿ���������y=| k |
| x |
| k |
| x |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
 ��COA=45�㣬����P�ӵ�O������������OABC�ı����˶���·��ΪO��A��B��C�������Cʱֹͣ����ֱ��CP��
��COA=45�㣬����P�ӵ�O������������OABC�ı����˶���·��ΪO��A��B��C�������Cʱֹͣ����ֱ��CP���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com