
【题目】如图,△![]() 中,
中,![]() 、
、![]() 的角平分线
的角平分线![]() 、
、![]() 交于点
交于点![]() ,延长
,延长![]() 、
、![]() ,
,![]() ,
,![]() ,则下列结论中正确的个数是( )
,则下列结论中正确的个数是( )
①CP平分∠ACF; ②∠ABC+2∠APC=180°;
③∠ACB=2∠APB; ④若PM⊥BE,PN⊥BC,则AM+CN=AC;
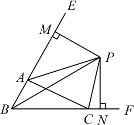
A.1个B.2个C.3个D.4个
【答案】D
【解析】
①作PD⊥AC于D.由角平分线的性质得出PM=PN,PM=PD,得出PM=PN=PD,即可得出①正确;
②首先证出∠ABC+∠MPN=180°,证明Rt△PAM≌Rt△PAD(HL),得出∠APM=∠APD,同理:Rt△PCD≌Rt△PCN(HL),得出∠CPD=∠CPN,即可得出②正确;
③由角平分线和三角形的外角性质得出∠CAE=∠ABC+∠ACB,∠PAM=![]() ∠ABC+∠APB,得出∠ACB=2∠APB,③正确;
∠ABC+∠APB,得出∠ACB=2∠APB,③正确;
④由全等三角形的性质得出AD=AM,CD=CN,即可得出④正确;即可得出答案.
解:①作PD⊥AC于D.
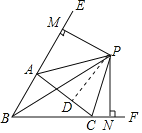
∵PB平分∠ABC,PA平分∠EAC,PM⊥BE,PN⊥BF,
∴PM=PN,PM=PD,
∴PM=PN=PD,
∴点P在∠ACF的角平分线上,故①正确;
②∵PM⊥AB,PN⊥BC,
∴∠ABC+90°+∠MPN+90°=360°,
∴∠ABC+∠MPN=180°,
在Rt△PAM和Rt△PAD中,
![]() ,
,
∴Rt△PAM≌Rt△PAD(HL),
∴∠APM=∠APD,
同理:Rt△PCD≌Rt△PCN(HL),
∴∠CPD=∠CPN,
∴∠MPN=2∠APC,
∴∠ABC+2∠APC=180°,②正确;
③∵PA平分∠CAE,BP平分∠ABC,
∴∠CAE=∠ABC+∠ACB,∠PAM=![]() ∠ABC+∠APB,
∠ABC+∠APB,
∴∠ACB=2∠APB,③正确;
④∵Rt△PAM≌Rt△PAD(HL),
∴AD=AM,
同理:Rt△PCD≌Rt△PCN(HL),
∴CD=CN,
∴AM+CN=AD+CD=AC,④正确;
故选:D.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,过点E作EF∥CD交BC的延长线于点F,连接CD.
(1)求证:DE=CF;
(2)求EF的长.
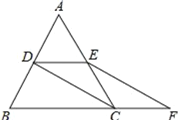
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC的平分线与∠ACB的外角的平分线相交于点P,连接AP.
(1)求证:PA平分∠BAC的外角∠CAM;
(2)过点C作CE⊥AP,E是垂足,并延长CE交BM于点D.求证:CE=ED.
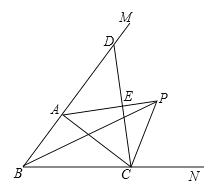
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:∠AOB=30°,点P是∠AOB 内部及射线OB上一点,且OP=10cm.
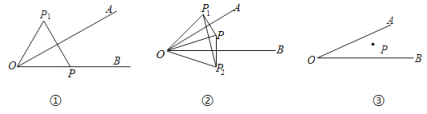
(1)若点P在射线OB上,过点P作关于直线OA的对称点![]() ,连接O
,连接O![]() 、P
、P![]() , 如图①求P
, 如图①求P![]() 的长.
的长.
(2)若过点P分别作关于直线OA、直线OB的对称点![]() 、
、![]() ,连接O
,连接O![]() 、O
、O![]() 、
、![]()
![]() 如图②, 求
如图②, 求![]()
![]() 的长.
的长.
(3)若点P在∠AOB 内,分别在射线OA、射线OB找一点M,N,使△PMN的周长取最小值,请直接写出这个最小值.如图③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有四张正面分别标有数字2,1,﹣3,﹣4的不透明卡片,它们除数字外其余全部相同,现将它们背面朝上,洗匀后从四张卡片中随机地摸取一张不放回,将该卡片上的数字记为m,再随机地摸取一张,将卡片上的数字记为n.
(1)请画出树状图并写出(m,n)所有可能的结果;
(2)求所选出的m,n能使一次函数y=mx+n的图象经过第二、三、四象限的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若关于x的一元二次方程(x–2)(x–3)=m有实数根x1、x2,且x1<x2,则下列结论中错误的是
A. 当m=0时,x1=2,x2=3
B. m>–![]()
C. 当m>0时,2<x1<x2<3
D. 二次函数y=(x–x1)(x–x2)+m的图象与x轴交点的坐标为(2,0)和(3,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题正确的是( )
A. 一组对边相等,另一组对边平行的四边形一定是平行四边形
B. 对角线相等的四边形一定是矩形
C. 两条对角线互相垂直的四边形一定是菱形
D. 两条对角线相等且互相垂直平分的四边形一定是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
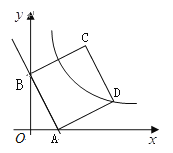
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别相交于点A和B.
轴分别相交于点A和B.
(1)直接写出坐标:点A ,点B ;
(2)以线段AB为一边在第一象限内作□ABCD,其顶点D(![]() ,
, ![]() )在双曲线
)在双曲线![]() (
(![]() >
>![]() )上.
)上.
①求证:四边形ABCD是正方形;
②试探索:将正方形ABCD沿![]() 轴向左平移多少个单位长度时,点C恰好落在双曲线
轴向左平移多少个单位长度时,点C恰好落在双曲线![]() (
(![]() >
>![]() )上.
)上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com