
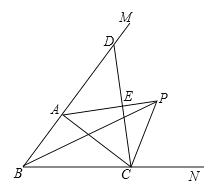
【题目】如图,在△ABC中,∠ABC的平分线与∠ACB的外角的平分线相交于点P,连接AP.
(1)求证:PA平分∠BAC的外角∠CAM;
(2)过点C作CE⊥AP,E是垂足,并延长CE交BM于点D.求证:CE=ED.
【答案】(1)见解析;(2)见解析
【解析】
(1)过P作PT⊥BC于T,PS⊥AC于S,PQ⊥BA于Q,根据角平分线性质求出PQ=PS=PT,根据角平分线性质得出即可;
(2)根据ASA求出△AED≌△AEC即可.
解:证明:(1)过P作PT⊥BC于T,PS⊥AC于S,PQ⊥BA于Q,如图,
∵在△ABC中,∠ABC的平分线与∠ACB的外角的平分线相交于点P,
∴PQ=PT,PS=PT,
∴PQ=PS,
∴AP平分∠DAC,
即PA平分∠BAC的外角∠CAM;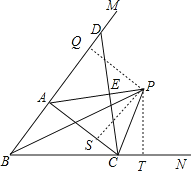
(2)∵PA平分∠BAC的外角∠CAM,
∴∠DAE=∠CAE,
∵CE⊥AP,
∴∠AED=∠AEC=90°,
在△AED和△AEC中,
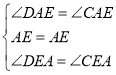 ,
,
∴△AED≌△AEC(ASA),
∴CE=ED.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图1:在平面直角坐标系内,O为坐标原点,线段AB两端点在坐标轴上且点A(﹣4,0),点B(0,3),将AB向右平移4个单位长度至OC的位置
(1)直接写出点C的坐标 ;
(2)如图2,过点C作CD⊥x轴于点D,在x轴正半轴有一点E(1,0),过点E作x轴的垂线,在垂线上有一动点P,直接写出:①点D的坐标 ; ②三角形PCD的面积为 ;
(3)如图3,在(2)的条件下,连接AC,当△ACP的面积为![]() 时,直接写出点P的坐标 .
时,直接写出点P的坐标 .

查看答案和解析>>
科目:初中数学 来源: 题型:
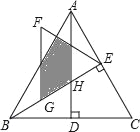
【题目】如图,△ABC是等边三角形,高AD、BE相交于点H,BC=4![]() ,在BE上截取BG=2,以GE为边作等边三角形GEF,则△ABH与△GEF重叠(阴影)部分的面积为_____.
,在BE上截取BG=2,以GE为边作等边三角形GEF,则△ABH与△GEF重叠(阴影)部分的面积为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按要求完成下列视图问题

(1)如图(一),它是由![]() 个同样大小的正方体摆成的几何体.将正方体①移走后,新几何体的三视图与原几何体的三视图相比,哪一个视图没有发生改变?
个同样大小的正方体摆成的几何体.将正方体①移走后,新几何体的三视图与原几何体的三视图相比,哪一个视图没有发生改变?
(2)如图(二),请你借助虚线网格(甲)画出该几何体的俯视图.
(3)如图(三),它是由几个小立方块组成的俯视图,小正方形上的数字表示该位置上的正方体的个数,请你借助虚线网格(乙)画出该几何体的主视图.
(4)如图(四),它是由![]() 个大小相同的正方体组成的几何体的主视图和俯视图,请你借助虚线网格(丙)画出该几何体的左视图.
个大小相同的正方体组成的几何体的主视图和俯视图,请你借助虚线网格(丙)画出该几何体的左视图.
查看答案和解析>>
科目:初中数学 来源: 题型:
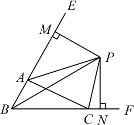
【题目】如图,△![]() 中,
中,![]() 、
、![]() 的角平分线
的角平分线![]() 、
、![]() 交于点
交于点![]() ,延长
,延长![]() 、
、![]() ,
,![]() ,
,![]() ,则下列结论中正确的个数是( )
,则下列结论中正确的个数是( )
①CP平分∠ACF; ②∠ABC+2∠APC=180°;
③∠ACB=2∠APB; ④若PM⊥BE,PN⊥BC,则AM+CN=AC;
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
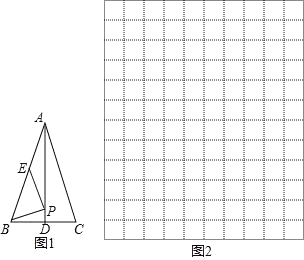
【题目】如图 1,在等腰△ABC 中,AB=AC,点 D,E 分别为 BC,AB 的中点,连接 AD.在线段 AD 上任取一点 P,连接 PB,PE.若 BC=4,AD=6,设 PD=x(当点 P 与点 D 重合时,x 的值为 0),PB+PE=y.
小明根据学习函数的经验,对函数y 随自变量x 的变化而变化的规律进行了探究. 下面是小明的探究过程,请补充完整:
(1)通过取点、画图、计算,得到了 x 与 y 的几组值,如下表:
x | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y | 5.2 | 4.2 | 4.6 | 5.9 | 7.6 | 9.5 |
说明:补全表格时,相关数值保留一位小数.(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732,
≈1.732,![]() ≈2.236)
≈2.236)
(2)建立平面直角坐标系(图 2),描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
(3)求函数 y 的最小值(保留一位小数),此时点 P 在图 1 中的什么位置.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com