
【题目】如图1,已知△ABC中,AB=BC=1,∠ABC=90°,把一块含30°角的直角三角板DEF的直角顶点D放在AC的中点上(直角三角板的短直角边为DE,长直角边为DF),将直角三角板DEF绕D点按逆时针方向旋转.
(1)在图1中,DE交AB于M,DF交BC于N.
①求证:DM=DN;
②在这一旋转过程中,直角三角板DEF与△ABC的重叠部分为四边形DMBN,请说明四边形DMBN的面积是否发生变化?若发生变化,请说明是如何变化的?若不发生变化,求出其面积;
(2)继续旋转至如图2的位置,延长AB交DE于M,延长BC交DF于N,DM=DN是否仍然成立?若成立,请给出证明;若不成立,请说明理由;
(3)继续旋转至如图3的位置,延长FD交BC于N,延长ED交AB于M,DM=DN是否仍然成立?请写出结论,不用证明.

【答案】(1)①证明详见解析;②四边形DMBN的面积不发生变化,理由详见解析;
(2)DM=DN仍然成立,理由详见解析;(3)DM=DN.
【解析】
试题分析:(1)①连接DB,根据AAS证明△BMD≌△CND,所以DM=DN;
②由①知△BMD≌△CND,所以![]() ,所以四边形DMBN的面积等于△ABC的面积的一半;
,所以四边形DMBN的面积等于△ABC的面积的一半;
(2)连接DB,依然可以证得△BMD≌△CND,所以DM=DN;
(3)根据(2)的思路可以得到DM=DN.
试题解析:(1)①证明:连接DB,
在Rt△ABC中,因为AB=BC,AD=DC,所以DB=DC=AD,∠BDC=90°,
所以∠ABD=∠C=45°,
因为∠MDB+∠BDN=∠CDN+∠BDN=90°,
所以∠MDB=∠NDC,
所以△BMD≌△CND,所以DM=DN.
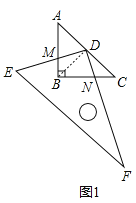
②四边形DMBN的面积不发生变化,理由如下:
由①知△BMD≌△CND,所以![]() ,所以
,所以![]() =
=![]() =
=![]() .
.
(2)DM=DN仍然成立,理由如下:
连接DB,在Rt△ABC中,因为AB=BC,AD=DC,所以DB=DC=AD,∠BDC=90°,所以∠DCB=∠DBC=45°,所以∠DBM=∠DCN=135°,因为∠NDC+∠CDM=∠BDM+∠CDM=90°,所以∠MDB=∠NDC,所以△BMD≌△CND,所以DM=DN.
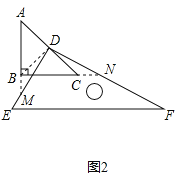
(3) DM=DN.


科目:初中数学 来源: 题型:
【题目】求1+2+22+23+…+22018的值,可令S=1+2+22+23+…+22018,则2S=2+22+23+24+…22019,因此2S﹣S=22019﹣1,即S=22019﹣1.依照以上的方法,计算出1+5+52+53+…52017的值为( )
A. 52018﹣1 B. 52019﹣1 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一数轴上存在两动点,当第一次相遇后,速度都变为原来的两倍,第二次相遇后又都能恢复到原来的速度,则称这条数轴为魔幻数轴.
如图,已知一魔幻数轴上有A,O,B三点,其中A,O对应的数分别为﹣10,0,AB为47个单位长度,甲,乙分别从A,O两点同时出发,沿数轴正方向同向而行,甲的速度为3个单位/秒,乙的速度为1个单位/秒,甲到达点B后以当时速度立即返回,当甲回到点A时,甲、乙同时停止运动.
![]()
问:(1)点B对应的数为 ,甲出发 秒后追上乙(即第一次相遇)
(2)当甲到达点B立即返回后第二次与乙相遇,求出相遇点在数轴上表示的数是多少?
(3)甲、乙同时出发多少秒后,二者相距2个单位长度?(请直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,∠AOB=90°,∠OAB=30°,反比例函数y1=![]() 的图象经过点A,反比例函数y2=
的图象经过点A,反比例函数y2=![]() 的图象经过点B,则下列关于m,n的关系正确的是( )
的图象经过点B,则下列关于m,n的关系正确的是( )

A. m=-3n B. m=-![]() n C. m=-
n C. m=-![]() n D. m=
n D. m=![]() n
n
查看答案和解析>>
科目:初中数学 来源: 题型:
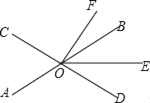
【题目】如图,直线AB、CD相交于点O,OE平分∠BOD.
(1)若∠AOC=68°,∠DOF=90°,求∠EOF的度数.
(2)若OF平分∠COE,∠BOF=30°,求∠AOC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C是⊙O上一点,过点C的直线交AB的延长线于点D,AE⊥DC,垂足为E,F是AE与⊙O的交点,AC平分∠BAE.

(1)求证:DE是⊙O的切线;
(2)若AE=6,∠D=30°,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() ,则下列结论正确的是( )
,则下列结论正确的是( )
A. 其图象分别位于第一、三象限
B. 当![]() 时,
时,![]() 随
随![]() 的增大而减小
的增大而减小
C. 若点![]() 在它的图象上,则点
在它的图象上,则点![]() 也在它的图象上
也在它的图象上
D. 若点![]() 都在该函数图象上,且
都在该函数图象上,且![]() ,则
,则![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C是⊙O上一点,过点C的直线交AB的延长线于点D,AE⊥DC,垂足为E,F是AE与⊙O的交点,AC平分∠BAE.

(1)求证:DE是⊙O的切线;
(2)若AE=6,∠D=30°,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中
中![]() 且
且![]() ,又
,又![]() 、
、![]() 为
为![]() 的三等分点.
的三等分点.

(1)求证![]() ;
;
(2)证明:![]() ;
;
(3)若点![]() 为线段
为线段![]() 上一动点,连接
上一动点,连接![]() 则使线段
则使线段![]() 的长度为整数的点的个数________.(直接写答案无需说明理由)
的长度为整数的点的个数________.(直接写答案无需说明理由)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com