Question

3．（1）请你根据下面画图要求，在图①中完成画图操作并填空．
如图①，△ABC中，∠BAC=30°，∠ACB=90°，∠PAM=∠A．
操作：（1）延长BC．
（2）将∠PAM绕点A逆时针方向旋转60°后，射线AM交BC的延长线于点D．
（3）过点D作DQ∥AB．
（4）∠PAM旋转后，射线AP交DQ于点G．
（5）连结BG．
结论：$\frac{AB}{AG}$=$\frac{1}{2}$．
（2）如图②，△ABC中，AB=AC=1，∠BAC=36°，进行如下操作：将△ABC绕点A按逆时针方向旋转α度角，并使各边长变为原来的n倍（n＞1），得到△AB′C′．当点B、C、B′在同一条直线上，且四边形ABB′C′为平行四边形时（如图③），求a和n的值．

Answer 1

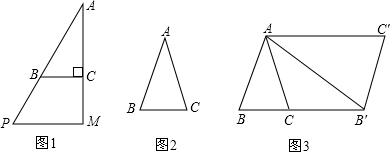
分析 （1）根据旋转得出△ABC～△AGD，设AB为2，根据30°的直角三角形的性质得出AD=2$\sqrt{3}$，进一步得出AG=4，可得$\frac{AB}{AG}$=$\frac{1}{2}$；
（2）由四边形ABB′C′是平行四边形，易求得a=36°，又由△ABC∽△AB′C′，根据相似三角形的对应边成比例，继而求得答案．

解答 解：（1）如图：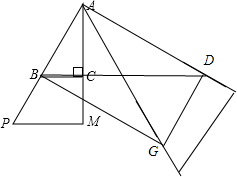
∵∠BAC=30°，∠ACB=90°，
∴∠PAM=∠A=30°，
∵∠PAM绕点A逆时针方向旋转60°，
∴∠BAG=60°，△ABC～△AGD，
∴∠GAD=∠BAC=∠MAG=30°，
∴△BAD是Rt△，∠ABD=60°，
∴∠ADB=30°，
设AB为2，则可得AD=$2\sqrt{3}$，
∵DQ∥AB，∠BAD=90°
∴∠ADG=90°，
∵∠GAD=30°，AD=$2\sqrt{3}$，
∴AG=4，
∴$\frac{AB}{AG}$=$\frac{2}{4}=\frac{1}{2}$；

（2）∵四边形ABB′C′是平行四边形，
∴AC′∥BB′，
又∵∠BAC=36°，AB=AC
∴∠ABC=72°．
∴∠B′AC′=∠BAC=36°，
∴∠CAB′=36°，
∴α=180°-72°-36°=72°；
∴∠B′AC′=∠BAC=36°，而∠B=∠AB′C′，
∴△ABC∽△AB′C′，
∴AB：BB′=CB：AB，
∴AB²=CB•AB′，
而 AB=1，
BC=2ABsin18°≈0.618，
所以可得n=$\frac{AB′}{BC}=\frac{\frac{1}{0.618}}{0.618}≈2.62$．

点评 此题考查几何变换问题，关键是根据直角三角形的性质得出边和角的关系，同时利用平行四边形的性质分析．