
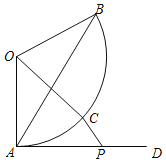
【题目】如图,在扇形AOB中,OA=OB=4,∠AOB=120°,点C是弧AB上的一个动点(不与点A,B重合),射线AD与扇形AOB所在⊙O相切,点P在射线AD上,连接AB,OC,CP,若AP=2![]() ,则CP的取值范围是_____.
,则CP的取值范围是_____.
【答案】![]()
【解析】
根据切线的性质得到∠OAD=90°,由OA=OB,得到∠OAB=30°,就可求出∠BAP,进而求出∠APB=90°,求出PB长.当O、C、P三点在一条直线上时,求出CP的长,则CP的取值范围可求出.
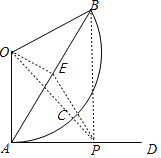
解:如图,当O、C、P三点在一条直线上时,
∵射线AD与扇形AOB所在⊙O相切,
∴∠OAP=90°,
∵AO=4,AP=![]() ,
,
∴![]() ,
,
∴PC=![]() ,
,
过点O作OE⊥AB于点E,连接PE、PB,
∵OA=OB=4,∠AOB=120°,
∴∠OAB=∠OBA=30°,
∴AE=BE=2![]() ,∠BAP=60°,
,∠BAP=60°,
∴AE=AP,
∴△AEP是等边三角形,
∴∠AEP=60°,
∴∠EPB=30°,
∴∠APB=90°,
∴![]() ,
,
∵点C不与A、B重合,
∴PC的取值范围是![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】如图所示,△ADB≌△EDB,△BDE≌△CDE,B,E,C在一条直线上.下列结论:①BD是∠ABE的平分线;②AB⊥AC;③∠C=30°;④线段DE是△BDC的中线;⑤AD+BD=AC.其中正确的有( )个.

A.2B.3C.4D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=![]() x2+bx+c的图象过点B(0,1)和C(4,3)两点,与x轴交于点D、点E,过点B和点C的直线与x轴交于点A.
x2+bx+c的图象过点B(0,1)和C(4,3)两点,与x轴交于点D、点E,过点B和点C的直线与x轴交于点A.
(1)求二次函数的解析式;
(2)在x轴上有一动点P,随着点P的移动,存在点P使△PBC是直角三角形,请你求出点P的坐标;
(3)若动点P从A点出发,在x轴上沿x轴正方向以每秒2个单位的速度运动,同时动点Q也从A点出发,以每秒a个单位的速度沿射线AC运动,是否存在以A、P、Q为顶点的三角形与△ABD相似?若存在,直接写出a的值;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
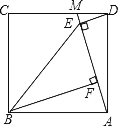
【题目】如图,点M是正方形ABCD边CD上一点,连接AM,作DE⊥AM于点E,BF⊥AM于点F,连接BE,若AF=1,四边形ABED的面积为6,则∠EBF的余弦值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
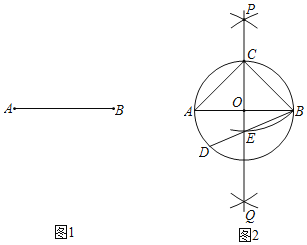
【题目】对于长度为4的线段AB(图1),小若用尺规进行如下操作(图2)根据作图痕迹,有下列说法:①△ABC是等腰三角形;②△ABC是直角三角形;③△ABC是等边三角形;④弧AD的长度为![]() ,⑤△ABC是直角三角形的依据是直径所对的圆周角为直角,则其中正确的个数是( )
,⑤△ABC是直角三角形的依据是直径所对的圆周角为直角,则其中正确的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某药品生产基地共有5条生产线,每条生产线每月生产药品20万盒,该基地打算从第一个月开始到第五个月结束,对每条生产线进行升级改造.改造时,每个月只升级改造一条生产线,这条生产线当月停产,并于下个月投入生产,其他生产线则正常生产.经调查,每条生产线升级改造后,每月的产量会比原来提高20%.
(1)根据题意,完成下面问题:
①把下表补充完整(直接写在横线上):
月数 | 第1个月 | 第2个月 | 第3个月 | 第4个月 | 第5个月 | 第6个月 | … |
产量/万盒 |
|
|
| 92 | … | … | … |
②从第1个月进行升级改造后,第 个月的产量开始超过未升级改造时的产量;
(2)若该基地第x个月(1≤x≤5,且x是整数)的产量为y万盒,求y关于x的函数关系式;
(3)已知每条生产线的升级改造费是30万元,每盒药品可获利3元.设从第1个月开始升级改造后,生产药品所获总利润为W1万元;同时期内,不升级改造所获总利润为W2万元设至少到第n个月(n为正整数)时,W1大于W2,求n的值.(利润=获利﹣改造费)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形AOBC中,O为坐标原点,OA、OB分别在x轴、y轴上,点B的坐标为(0,3),∠ABO=30°,将△ABC沿AB所在直线对折后,点C落在点D处,则点D的坐标为____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是菱形ABCD边上的动点,它从点A出发沿A→B→C→D路径匀速运动到点D,设![]() 的面积为y,P点的运动时间为x,则y关于x的函数图象大致为( )
的面积为y,P点的运动时间为x,则y关于x的函数图象大致为( )
A.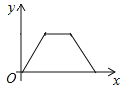 B.
B.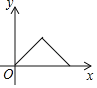 C.
C.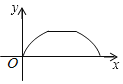 D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
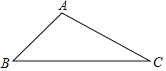
【题目】超速行驶被称为“马路第一杀手”,为了让驾驶员自觉遵守交通规则,市公路检测中在一事故多发地段安装了一个测速仪器,如图所示,已知检测点A设在距离公路BC20米处,∠B=45°,∠C=30°,现测得一辆汽车从B处行驶到C处所用时间为2.7秒.
(1)求B,C之间的距离(结果保留根号);
(2)如果此地限速为80km/h,那么这辆汽车是否超速?请说明理由.(参考数据:![]() 1.7,
1.7,![]() ≈1.4)
≈1.4)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com