
【题目】如图,在矩形AOBC中,O为坐标原点,OA、OB分别在x轴、y轴上,点B的坐标为(0,3),∠ABO=30°,将△ABC沿AB所在直线对折后,点C落在点D处,则点D的坐标为____________.

【答案】(![]() ,
,![]() )
)
【解析】
过点D作DE⊥y轴于E,根据矩形的性质可得∠CBO=∠BOA=90°,OB=3,AO=BC,然后根据锐角三角函数即可求出AO和BC,再根据折叠的性质可得BD=BC=![]() ,∠ABD=∠CBA=60°,然后利用锐角三角函数求出BE和ED,即可求出OE,从而求出点D的坐标.
,∠ABD=∠CBA=60°,然后利用锐角三角函数求出BE和ED,即可求出OE,从而求出点D的坐标.
解:过点D作DE⊥y轴于E

∵四边形AOBC是矩形,点B的坐标为(0,3),∠ABO=30°,
∴∠CBO=∠BOA=90°,OB=3,AO=BC
∴∠CBA=∠CBO-∠ABO=60°,
在Rt△BAO中,AO=OB·tan∠ABO=![]()
∴BC=![]()
根据折叠的性质可知BD=BC=![]() ,∠ABD=∠CBA=60°
,∠ABD=∠CBA=60°
∴∠EBD=∠ABD-∠ABO=30°
在Rt△EBD中,DE=BD·sin∠EBD=![]() ,BE=BD·cos∠EBD=
,BE=BD·cos∠EBD=![]()
∴OE=OB-BE=![]()
∴点D的坐标为(![]() ,
,![]() )
)
故答案为:(![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
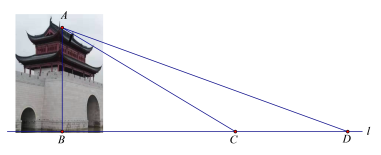
【题目】水城门位于淀浦河和漕港河三叉口,是环城水系公园淀浦河梦蝶岛区域重要的标志性景观.在课外实践活动中,某校九年级数学兴趣小组决定测量该水城门的高.他们的操作方法如下:如图,先在D处测得点A的仰角为20°,再往水城门的方向前进13米至C处,测得点A的仰角为31°(点D、C、B在一直线上),求该水城门AB的高.(精确到0.1米)
(参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,
,![]() ,直线
,直线![]() 与抛物线交于点
与抛物线交于点![]() ,
,![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
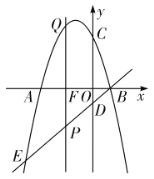
(1)求抛物线的解析式;
(2)点![]() 是线段
是线段![]() 上的一动点(不与
上的一动点(不与![]() ,
,![]() 重合),过点
重合),过点![]() 作
作![]() 轴的垂线,交
轴的垂线,交![]() 轴于点
轴于点![]() ,交抛物线于点
,交抛物线于点![]() ,若
,若![]() ,线段
,线段![]() 是否存在最大值?若存在,请求出最大值,若不存在,请说明理由;
是否存在最大值?若存在,请求出最大值,若不存在,请说明理由;
(3)若![]() 轴上存在一点
轴上存在一点![]() ,使得
,使得![]() 时,求出点
时,求出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
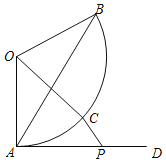
【题目】如图,在扇形AOB中,OA=OB=4,∠AOB=120°,点C是弧AB上的一个动点(不与点A,B重合),射线AD与扇形AOB所在⊙O相切,点P在射线AD上,连接AB,OC,CP,若AP=2![]() ,则CP的取值范围是_____.
,则CP的取值范围是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
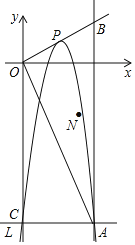
【题目】如图,点P为抛物线L:y=a(x﹣2)(x﹣4)(其中a为常数,且a<0)的顶点,L与y轴交于点C,过点C作x轴的平行线,与L交于点A,过点A作x轴的垂线,与射线OP交于点B,连接OA
(1)a=﹣2时,点P的坐标是 ,点B的坐标是 ;
(2)是否存在a的值,使OA=OB?若存在,求出a的值;若不存在,请说明理由
(3)若△OAB的外心N的坐标为(p,q),则
①当点N在△OAB内部时,求a的取值范围;
②用a表示外心N的横坐标p和纵坐标q,并求p与q的关系式(不写q的取值范围).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在直角坐标系中,直线l与x、y轴分别交于点A(2,0)、B(0,![]() )两点,∠BAO的角平分线交y轴于点D. 点C为直线l上一点,以AC为直径的⊙G经过点D,且与x轴交于另一点E.
)两点,∠BAO的角平分线交y轴于点D. 点C为直线l上一点,以AC为直径的⊙G经过点D,且与x轴交于另一点E.
(1)求出⊙G的半径r,并直接写出点C的坐标;
(2)如图2,若点F为⊙G上的一点,连接AF,且满足∠FEA=45°,请求出EF的长?
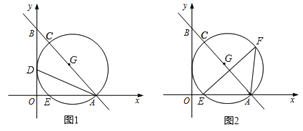
查看答案和解析>>
科目:初中数学 来源: 题型:
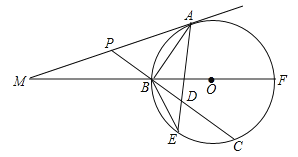
【题目】如图,已知BF是⊙O的直径,A为⊙O上(异于B、F)一点,⊙O的切线MA与FB的延长线交于点M;P为AM上一点,PB的延长线交⊙O于点C,D为BC上一点且PA=PD,AD的延长线交⊙O于点E.
(1)求证:![]() ;
;
(2)若ED、EA的长是一元二次方程![]() 的两根,求BE的长;
的两根,求BE的长;
(3)若MA=![]() ,sin∠AMF=
,sin∠AMF=![]() ,求AB的长.
,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义一种对正整数n的“C运算”:①当n为奇数时,结果为3n+1;②当n为偶数时,结果为![]() (其中k是使
(其中k是使![]() 为奇数的正整数)并且运算重复进行,例如,n=66时,其“C运算”如下:
为奇数的正整数)并且运算重复进行,例如,n=66时,其“C运算”如下:
![]()
若n=26,则第2019次“C运算”的结果是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
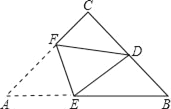
【题目】如图,在等腰直角△ABC中,∠C=90°,D为BC的中点,将△ABC折叠,使点A与点D重合,EF为折痕,则sin∠BED的值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com