Question

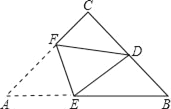
【题目】如图，在等腰直角△ABC中，∠C=90°，D为BC的中点，将△ABC折叠，使点A与点D重合，EF为折痕，则sin∠BED的值是（　　）

A. B. C. D.

Answer 1

【答案】B

【解析】分析：先根据翻折变换的性质得到△DEF≌△AEF，再根据等腰三角形的性质及三角形外角的性质可得到∠BED=CDF，设CD=1，CF=x，则CA=CB=2，再根据勾股定理即可求解．

详解：∵△DEF是△AEF翻折而成，

∴△DEF≌△AEF，∠A=∠EDF，

∵△ABC是等腰直角三角形，

∴∠EDF=45°，由三角形外角性质得∠CDF+45°=∠BED+45°，

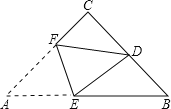
∴∠BED=∠CDF，

设CD=1，CF=x，则CA=CB=2，

∴DF=FA=2-x，

∴在Rt△CDF中，由勾股定理得，

CF2+CD2=DF2，

即x2+1=（2-x）2，

解得：x=，

∴sin∠BED=sin∠CDF=．

故选B．