
【题目】如图,一块四边形的纸板剪去△DEC,得到四边形ABCE,测得∠BAE =∠BCE=90°,BC=CE,AB=DE.

(1)能否在四边形纸板上只剪一刀,使剪下的三角形与△DEC全等?请说明理由;
(2)求∠D的度数.
【答案】(1)见解析(2)45°.
【解析】
(1)连接AC, 利用全等三角形的判定方法(SAS)进而判断得出答案.
(2)由第(1)△ABC≌△DEC,可得AC=DC, ∠ACB=∠DCE,根据∠BCE=90°, ∠ACB+∠ACE=∠BCE, ∠ACB=∠DCE,∠DCE+∠ACE=∠ACB+∠ACE=∠BCE=90°,
可得∠ACD=90°,继而可得△ADC是等腰直角三角形.
沿AC剪一刀.
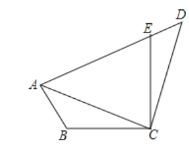
理由:∵∠BAE=∠BCE=90°,
∴∠ABC+∠AEC=180°,
∵∠AEC+∠DEC=180°,
∴∠DEC=∠B,
在△ABC和△DEC中,
AB=DE,∠B=∠EDC, BC=EC,
∴△ABC≌△DEC(SAS).
(2)∵△ABC≌△DEC,
∴AC=DC, ∠ACB=∠DCE,
∵∠BCE=90°, ∠ACB+∠ACE=∠BCE, ∠ACB=∠DCE,
∴∠DCE+∠ACE=∠ACB+∠ACE=∠BCE=90°,
∴∠ACD=90°,
∵AC=DC,
∴∠D=45°.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】已知关于x的方程![]() =1的解为负数,且关于x、y的二元一次方程组
=1的解为负数,且关于x、y的二元一次方程组![]() 的解之和为正数,则下列各数都满足上述条件a的值的是( )
的解之和为正数,则下列各数都满足上述条件a的值的是( )
A. ![]() ,2,5 B. 0,3,5 C. 3,4,5 D. 4,5,6
,2,5 B. 0,3,5 C. 3,4,5 D. 4,5,6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC≌Rt△CED(∠ACB=∠CDE=90°),点D在BC上,AB与CE相交于点F
(1) 如图1,直接写出AB与CE的位置关系
(2) 如图2,连接AD交CE于点G,在BC的延长线上截取CH=DB,射线HG交AB于K,求证:HK=BK


查看答案和解析>>
科目:初中数学 来源: 题型:
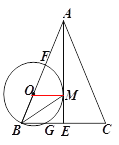
【题目】如图,在△ABC中,AB=AC,AE是BC边上的高线,BM平分∠ABC交AE于点M,经过B,M 两点的⊙O交BC于点G,交AB于点F ,FB为⊙O的直径.
(1)求证:AM是⊙O的切线
(2)当BE=3,cosC=![]() 时,求⊙O的半径.
时,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C是AB延长线上一点,CD与⊙O相切于点E,AD⊥CD于点D.

(1)求证:AE平分∠DAC;
(2)若AB=4,∠ABE=60°.
①求AD的长;
②求出图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
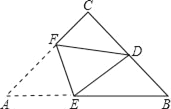
【题目】如图,在等腰直角△ABC中,∠C=90°,D为BC的中点,将△ABC折叠,使点A与点D重合,EF为折痕,则sin∠BED的值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com