
【题目】如图,Rt△ABC≌Rt△CED(∠ACB=∠CDE=90°),点D在BC上,AB与CE相交于点F
(1) 如图1,直接写出AB与CE的位置关系
(2) 如图2,连接AD交CE于点G,在BC的延长线上截取CH=DB,射线HG交AB于K,求证:HK=BK


【答案】(1)AB⊥CE;(2)见解析.
【解析】
(1)由全等可得∠ECD=∠A,再由∠B+∠A=90°,可得∠B+ECD=90°,则AB⊥CE.
(2)延长HK于DE交于H,易得△ACD为等腰直角三角形,∠ADC=45°,易得DH=DE,然后证明△DGH≌△DGE,所以∠H=∠E,则∠H=∠B,可得HK=BK.
解:(1)∵Rt△ABC≌Rt△CED,
∴∠ECD=∠A,∠B=∠E,BC=DE,AC=CD
∵∠B+∠A=90°
∴∠B+ECD=90°
∴∠BFC=90°,∴AB⊥CE
(2)在Rt△ACD中,AC=CD,∴∠ADC=45°,
又∵∠CDE=90°,∴∠HDG=∠CDG=45°
∵CH=DB,∴CH+CD=DB+CD,即HD=BC,
∴DH=DE,
在△DGH和△DGE中,

∴△DGH≌△DGE(SAS)
∴∠H=∠E
又∵∠B=∠E
∴∠H=∠B,
∴HK=BK


科目:初中数学 来源: 题型:
【题目】某校为了解八年级500名学生的身体健康情况,从该年级随机抽取了若干名学生,将他们按体重(均为整数,单位:kg)分成五组:A组:37.5~42.5,B组:42.5~47.5,C组:47.5~52.5,D组:52.5~57.5,E组:57.5~62.5,并依据统计数据绘制了如下两个不完整的统计图.

解答下列问题:
(1)这次抽样调查的样本容量是 ;在扇形统计图中D组的圆心角是 度.
(2)抽取的学生体重中位数落在 组;
(3)请你估计该校八年级体重超过52kg的学生大约有多少名?
(4)取每个小组的组中值作为本组学生的平均体重(A组的组中值为![]() ),请你估计该校八年级500名学生的平均体重.
),请你估计该校八年级500名学生的平均体重.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,直角△ABC 中,AC=BC,∠C=90°,∠CAB=∠ABC=45°,过点 B 作射线BD⊥AB 于 B,点 P 为 BC 边上任一点,在射线上取一点 Q,使得 PQ=AP.
(1)请依题意补全图形;
(2)试判断 AP 和 PQ 的位置关系,并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
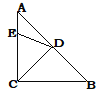
【题目】在等腰Rt△ABC中,D为斜边AB的中点,点E在AC上,且∠EDC=72°,点F在AB上,满足DE=DF,则∠CEF的度数为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线l:y=![]() x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=
x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=![]() x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
(1)求n的值和抛物线的解析式;
(2)点D在抛物线上,DE∥y轴交直线l于点E,点F在直线l上,且四边形DFEG为矩形(如图2),设点D的横坐标为t(0<t<4),矩形DFEG的周长为p,求p与t的函数关系式以及p的最大值;
(3)将△AOB绕平面内某点M旋转90°或180°,得到△A1O1B1,点A、O、B的对应点分别是点A1、O1、B1.若△A1O1B1的两个顶点恰好落在抛物线上,那么我们就称这样的点为“落点”,请直接写出“落点”的个数和旋转180°时点A1的横坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系中,A(a,0)、B(0,b),且|a+2|+(b+2a)2=0,点P为x轴上一动点,连接BP,在第一象限内作BC⊥AB且BC=AB
(1) 求点A、B的坐标
(2) 如图1,连接CP.当CP⊥BC时,作CD⊥BP于点D,求线段CD的长度
(3) 如图2,在第一象限内作BQ⊥BP且BQ=BP,连接PQ.设P(p,0),直接写出S△PCQ=_____

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一块四边形的纸板剪去△DEC,得到四边形ABCE,测得∠BAE =∠BCE=90°,BC=CE,AB=DE.

(1)能否在四边形纸板上只剪一刀,使剪下的三角形与△DEC全等?请说明理由;
(2)求∠D的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求∠F的度数;
(2)若CD=2,求DF的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com