
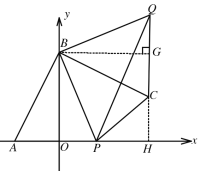
【题目】已知:如图,在平面直角坐标系中,A(a,0)、B(0,b),且|a+2|+(b+2a)2=0,点P为x轴上一动点,连接BP,在第一象限内作BC⊥AB且BC=AB
(1) 求点A、B的坐标
(2) 如图1,连接CP.当CP⊥BC时,作CD⊥BP于点D,求线段CD的长度
(3) 如图2,在第一象限内作BQ⊥BP且BQ=BP,连接PQ.设P(p,0),直接写出S△PCQ=_____

【答案】(1)A(-2,0),B(0,4);(2)CD=2;(3)![]()
【解析】
(1)由非负数的性质,可求出a、b的值,得到A、B的坐标;
(2)过C作CE⊥OB于E,与PB交于F,易证△AOB≌△BEC,可得OA=BE=2,即E为OB中点,所以EF为△BOP的中位线,F为Rt△BCP斜边BP上的中点,所以![]() ,所以∠BCF=∠CBD=∠ABO,再证△AOB≌△CDB即可得CD=OA.
,所以∠BCF=∠CBD=∠ABO,再证△AOB≌△CDB即可得CD=OA.
(3)过B作BG⊥CQ于点G,延长QC与x轴交于H,通过证△ABP≌△CBQ,△BOP≌△BGQ可推出OBGH为矩形,以CQ为底,PH为高求面积.
解:(1)∵|a+2|+(b+2a)2=0
∴a+2=0,b+2a=0,解得a=-2,b=4,
∴A(-2,0),B(0,4)
(2)如图所示,过C作CE⊥OB于E,与PB交于F,

∵BC⊥AB,∴∠ABO+∠EBC=90°,
在Rt△BCE中,∠EBC+∠BCE=90°,
∴∠ABO=∠BCE
在△AOB和△BEC中,

∴△AOB≌△BEC(AAS)
∴BE=AO=2,又∵OB=4,∴E为OB的中点,
∵EC∥OP,∴EF为△BOP的中位线,则F为BP的中点,
在Rt△BCP中,CF为斜边上的中线,
∴![]()
∴∠BCE=∠CBD=∠ABO
在△AOB和△CDB中

∴△AOB≌△CDB(AAS)
∴CD=AO=2
(3)如下图所示,过B作BG⊥CQ于点G,延长QC与x轴交于H,
∵∠ABP+∠PBC=90°,∠PBC+CBQ=90°,
∴∠ABP=∠CBQ
在△ABP与△CBQ中,

∴△ABP≌△CBQ(SAS)
∴∠BPO=∠BQG,CQ=AP=2+p,
在△BOP和△BGQ中,

∴△BOP≌△BGQ(AAS)
∴∠OBP=∠GBQ,BG=BO=4
又∵∠GBQ+∠PBG=90°
∴∠OBP+∠PBG=90°,即∠OBG=90°,
在四边形OBGH中,∠OBG=∠BOG=∠BGH=90°,
∴∠OHG=90°,∴PH是△PCQ中CQ边上的高,
PH=OH-OP=4-p
∴![]()


科目:初中数学 来源: 题型:
【题目】已知⊙O的直径AB=2,弦AC与弦BD交于点E.且OD⊥AC,垂足为点F.

(1)如图1,如果AC=BD,求弦AC的长;
(2)如图2,如果E为弦BD的中点,求∠ABD的余切值;
(3)联结BC、CD、DA,如果BC是⊙O的内接正n边形的一边,CD是⊙O的内接正(n+4)边形的一边,求△ACD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函双y=![]() (m≠0)的阳象交于点c(n,3),与x轴、y轴分别交于点A、B,过点C作CM⊥x轴,垂足为M,若tan∠CAM=
(m≠0)的阳象交于点c(n,3),与x轴、y轴分别交于点A、B,过点C作CM⊥x轴,垂足为M,若tan∠CAM=![]() ,OA=2.
,OA=2.
(1)求反比例函数和一次函数的解析式;
(2)点D是反比例函数图象在第三象限部分上的一点,且到x轴的距离是3,连接AD、BD,求△ABD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC≌Rt△CED(∠ACB=∠CDE=90°),点D在BC上,AB与CE相交于点F
(1) 如图1,直接写出AB与CE的位置关系
(2) 如图2,连接AD交CE于点G,在BC的延长线上截取CH=DB,射线HG交AB于K,求证:HK=BK


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E是正方形ABCD中CD边上一点,以点A为中心把△ADE顺时针旋转90°。

(1)在图中画出旋转后的图形;
(2)若旋转后E点的对应点记为M,点F在BC上,且∠EAF=45°,连接EF。
①求证:△AMF≌△AEF;
②若正方形的边长为6,AE=![]() ,求EF的长.
,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
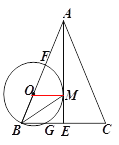
【题目】如图,在△ABC中,AB=AC,AE是BC边上的高线,BM平分∠ABC交AE于点M,经过B,M 两点的⊙O交BC于点G,交AB于点F ,FB为⊙O的直径.
(1)求证:AM是⊙O的切线
(2)当BE=3,cosC=![]() 时,求⊙O的半径.
时,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某乡镇要在生活垃圾存放区建一个老年活动中心,这样必须把1200立方米的生活垃圾运走:
(1)假如每天能运x立方米,所需时间为y天,写出y与x之间的函数表达式;
(2)若每辆拖拉机一天能运12立方米,则5辆这样的拖拉机要用多少天才能运完?
(3)在(2)的情况下,运了8天后,剩下的任务要在不超过6天的时间内完成,那么至少需要增加多少辆这样的拖拉机才能按时完成任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC与△CDE都是等边三角形,AD与BE相交于点G,BE与AC相交于点F,AD与CE相交于点H,则下列结论:①△ACD≌△BCE;②∠AFB=60°;③BF=AH;④△ECF≌△DCG;⑤连CG,则∠BGC=∠DGC.其中正确的个数是()

A.1个B.2个C.3个D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com