
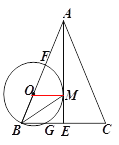
【题目】如图,在△ABC中,AB=AC,AE是BC边上的高线,BM平分∠ABC交AE于点M,经过B,M 两点的⊙O交BC于点G,交AB于点F ,FB为⊙O的直径.
(1)求证:AM是⊙O的切线
(2)当BE=3,cosC=![]() 时,求⊙O的半径.
时,求⊙O的半径.
科目:初中数学 来源: 题型:
【题目】如图,有8×8的正方形网格,每个小正方形边长为1,按要求操作并计算。
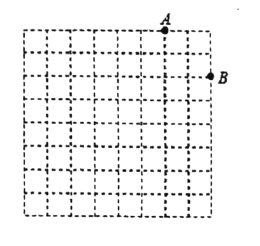
(1)在8×8的正方形网格中建立平面直角坐标系,使点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ;
;
(2)将点![]() 向下平移5个单位,再关于
向下平移5个单位,再关于![]() 轴对称得到点
轴对称得到点![]() ,则点
,则点![]() 坐标为(_______,_________);
坐标为(_______,_________);
(3)画出三角形![]() ,并求其面积。
,并求其面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
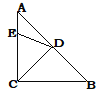
【题目】在等腰Rt△ABC中,D为斜边AB的中点,点E在AC上,且∠EDC=72°,点F在AB上,满足DE=DF,则∠CEF的度数为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系中,A(a,0)、B(0,b),且|a+2|+(b+2a)2=0,点P为x轴上一动点,连接BP,在第一象限内作BC⊥AB且BC=AB
(1) 求点A、B的坐标
(2) 如图1,连接CP.当CP⊥BC时,作CD⊥BP于点D,求线段CD的长度
(3) 如图2,在第一象限内作BQ⊥BP且BQ=BP,连接PQ.设P(p,0),直接写出S△PCQ=_____

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一块四边形的纸板剪去△DEC,得到四边形ABCE,测得∠BAE =∠BCE=90°,BC=CE,AB=DE.

(1)能否在四边形纸板上只剪一刀,使剪下的三角形与△DEC全等?请说明理由;
(2)求∠D的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求∠F的度数;
(2)若CD=2,求DF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,AB=8,AC=4,D是AB边上一点,P是优弧![]() 的中点,连接PA,PB,PC,PD,当BD的长度为多少时,△PAD是以AD为底边的等腰三角形?并加以证明.
的中点,连接PA,PB,PC,PD,当BD的长度为多少时,△PAD是以AD为底边的等腰三角形?并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明沿街道匀速行走,他注意到每隔6分钟从背后驶过一辆1路公交车,每隔4分钟迎面驶来一辆1路公交车.假设每辆1路公交车行驶速度相同,而且1路公交车总站每隔固定时间发一辆车,那么发车间隔的时间是________分钟.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com