
【题目】如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函双y=![]() (m≠0)的阳象交于点c(n,3),与x轴、y轴分别交于点A、B,过点C作CM⊥x轴,垂足为M,若tan∠CAM=
(m≠0)的阳象交于点c(n,3),与x轴、y轴分别交于点A、B,过点C作CM⊥x轴,垂足为M,若tan∠CAM=![]() ,OA=2.
,OA=2.
(1)求反比例函数和一次函数的解析式;
(2)点D是反比例函数图象在第三象限部分上的一点,且到x轴的距离是3,连接AD、BD,求△ABD的面积.

科目:初中数学 来源: 题型:
【题目】方格纸中每个小方格都是边长为1的正方形,我们把以格点连线为边的多边形称为“格点多边形”.

(1)在图1中确定格点D,并画出一个以A、B、C、D为顶点的四边形,使其为轴对称图形(一种情况即可);
(2)直接写出图2中△FGH的面积是 ;
(3)在图3中画一个格点正方形,使其面积等于17.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函双y=![]() (m≠0)的阳象交于点c(n,3),与x轴、y轴分别交于点A、B,过点C作CM⊥x轴,垂足为M,若tan∠CAM=
(m≠0)的阳象交于点c(n,3),与x轴、y轴分别交于点A、B,过点C作CM⊥x轴,垂足为M,若tan∠CAM=![]() ,OA=2.
,OA=2.
(1)求反比例函数和一次函数的解析式;
(2)点D是反比例函数图象在第三象限部分上的一点,且到x轴的距离是3,连接AD、BD,求△ABD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A是反比例函数y=![]() 的图象在第一象限上的动点,连结AO并延长交另一分支于点B,以AB为边作等边△ABC使点C落在第二象限,且边BC交x轴于点D,若△ACD与△ABD的面积之比为1:2,则点C的坐标为( )
的图象在第一象限上的动点,连结AO并延长交另一分支于点B,以AB为边作等边△ABC使点C落在第二象限,且边BC交x轴于点D,若△ACD与△ABD的面积之比为1:2,则点C的坐标为( )

A. (﹣3,2![]() ) B. (﹣5,
) B. (﹣5,![]() ) C. (﹣6,
) C. (﹣6,![]() ) D. (﹣3
) D. (﹣3![]() ,2)
,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
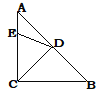
【题目】在等腰Rt△ABC中,D为斜边AB的中点,点E在AC上,且∠EDC=72°,点F在AB上,满足DE=DF,则∠CEF的度数为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,点E、F分别在BC、CD上,将△ABE沿AE折叠,使点B落在AC上的点Bˊ处,又将△CEF沿EF折叠,使点C落在射线EBˊ与AD的交点Cˊ处,则![]() 的值( )
的值( )

A. 2 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系中,A(a,0)、B(0,b),且|a+2|+(b+2a)2=0,点P为x轴上一动点,连接BP,在第一象限内作BC⊥AB且BC=AB
(1) 求点A、B的坐标
(2) 如图1,连接CP.当CP⊥BC时,作CD⊥BP于点D,求线段CD的长度
(3) 如图2,在第一象限内作BQ⊥BP且BQ=BP,连接PQ.设P(p,0),直接写出S△PCQ=_____

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB=120°,OP平分∠AOB,且OP=2.若点M,N分别在OA,OB上,且△PMN为等边三角形,则满足上述条件的△PMN有( )

A.1个B.2个C.3个D.3个以上
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com