
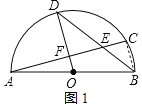
【题目】已知⊙O的直径AB=2,弦AC与弦BD交于点E.且OD⊥AC,垂足为点F.

(1)如图1,如果AC=BD,求弦AC的长;
(2)如图2,如果E为弦BD的中点,求∠ABD的余切值;
(3)联结BC、CD、DA,如果BC是⊙O的内接正n边形的一边,CD是⊙O的内接正(n+4)边形的一边,求△ACD的面积.
【答案】(1)AC=![]() ;(2)cot∠ABD=
;(2)cot∠ABD=![]() ;(3)S△ACD=
;(3)S△ACD=![]() .
.
【解析】(1)由AC=BD知![]() ,得
,得![]() ,根据OD⊥AC知
,根据OD⊥AC知![]() ,从而得
,从而得![]() ,即可知∠AOD=∠DOC=∠BOC=60°,利用AF=AOsin∠AOF可得答案;
,即可知∠AOD=∠DOC=∠BOC=60°,利用AF=AOsin∠AOF可得答案;
(2)连接BC,设OF=t,证OF为△ABC中位线及△DEF≌△BEC得BC=DF=2t,由DF=1﹣t可得t=![]() ,即可知BC=DF=
,即可知BC=DF=![]() ,继而求得EF=
,继而求得EF=![]() AC=
AC=![]() ,由余切函数定义可得答案;
,由余切函数定义可得答案;
(3)先求出BC、CD、AD所对圆心角度数,从而求得BC=AD=![]() 、OF=
、OF=![]() ,从而根据三角形面积公式计算可得.
,从而根据三角形面积公式计算可得.
(1)∵OD⊥AC,
∴![]() ,∠AFO=90°,
,∠AFO=90°,
又∵AC=BD,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴∠AOD=∠DOC=∠BOC=60°,
∵AB=2,
∴AO=BO=1,
∴AF=AOsin∠AOF=1×![]() =
=![]() ,
,
则AC=2AF=![]() ;
;
(2)如图1,连接BC,
∵AB为直径,OD⊥AC,
∴∠AFO=∠C=90°,
∴OD∥BC,
∴∠D=∠EBC,
∵DE=BE、∠DEF=∠BEC,
∴△DEF≌△BEC(ASA),
∴BC=DF、EC=EF,
又∵AO=OB,
∴OF是△ABC的中位线,
设OF=t,则BC=DF=2t,
∵DF=DO﹣OF=1﹣t,
∴1﹣t=2t,
解得:t=![]() ,
,
则DF=BC=![]() 、AC=
、AC=![]() =
=![]() ,
,
∴EF=![]() FC=
FC=![]() AC=
AC=![]() ,
,
∵OB=OD,
∴∠ABD=∠D,
则cot∠ABD=cot∠D=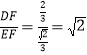 ;
;
(3)如图2,
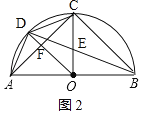
∵BC是⊙O的内接正n边形的一边,CD是⊙O的内接正(n+4)边形的一边,
∴∠BOC=![]() 、∠AOD=∠COD=
、∠AOD=∠COD=![]() ,
,
则![]() +2×
+2×![]() =180,
=180,
解得:n=4,
∴∠BOC=90°、∠AOD=∠COD=45°,
∴BC=AC=![]() ,
,
∵∠AFO=90°,
∴OF=AOcos∠AOF=![]() ,
,
则DF=OD﹣OF=1﹣![]() ,
,
∴S△ACD=![]() ACDF=
ACDF=![]() ×
×![]() ×(1﹣
×(1﹣![]() )=
)=![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,一个正比例函数与一个一次函数的图象交于点A(3,4),其中一次函数与y轴交于B点,且OA=OB.

(1)求这两个函数的表达式;
(2)求△AOB的面积S.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线a∥b,且a与b之间的距离为4,点A到直线a的距离为2,点B到直线b的距离为3,AB=![]() .试在直线a上找一点M,在直线b上找一点N,满足MN⊥a且AM+MN+NB的长度和最短,则此时AM+NB=
.试在直线a上找一点M,在直线b上找一点N,满足MN⊥a且AM+MN+NB的长度和最短,则此时AM+NB=

A.6 B.8 C.10 D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】方格纸中每个小方格都是边长为1的正方形,我们把以格点连线为边的多边形称为“格点多边形”.

(1)在图1中确定格点D,并画出一个以A、B、C、D为顶点的四边形,使其为轴对称图形(一种情况即可);
(2)直接写出图2中△FGH的面积是 ;
(3)在图3中画一个格点正方形,使其面积等于17.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解八年级500名学生的身体健康情况,从该年级随机抽取了若干名学生,将他们按体重(均为整数,单位:kg)分成五组:A组:37.5~42.5,B组:42.5~47.5,C组:47.5~52.5,D组:52.5~57.5,E组:57.5~62.5,并依据统计数据绘制了如下两个不完整的统计图.

解答下列问题:
(1)这次抽样调查的样本容量是 ;在扇形统计图中D组的圆心角是 度.
(2)抽取的学生体重中位数落在 组;
(3)请你估计该校八年级体重超过52kg的学生大约有多少名?
(4)取每个小组的组中值作为本组学生的平均体重(A组的组中值为![]() ),请你估计该校八年级500名学生的平均体重.
),请你估计该校八年级500名学生的平均体重.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,直线l:y=![]() x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=
x+m与x轴、y轴分别交于点A和点B(0,﹣1),抛物线y=![]() x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
x2+bx+c经过点B,与直线l的另一个交点为C(4,n).
(1)求n的值和抛物线的解析式;
(2)点D在抛物线上,DE∥y轴交直线l于点E,点F在直线l上,且四边形DFEG为矩形(如图2),设点D的横坐标为t(0<t<4),矩形DFEG的周长为p,求p与t的函数关系式以及p的最大值;
(3)将△AOB绕平面内某点M旋转90°或180°,得到△A1O1B1,点A、O、B的对应点分别是点A1、O1、B1.若△A1O1B1的两个顶点恰好落在抛物线上,那么我们就称这样的点为“落点”,请直接写出“落点”的个数和旋转180°时点A1的横坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有8×8的正方形网格,每个小正方形边长为1,按要求操作并计算。
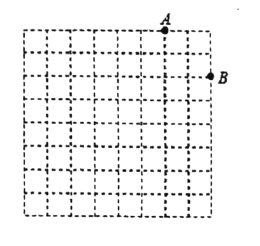
(1)在8×8的正方形网格中建立平面直角坐标系,使点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ;
;
(2)将点![]() 向下平移5个单位,再关于
向下平移5个单位,再关于![]() 轴对称得到点
轴对称得到点![]() ,则点
,则点![]() 坐标为(_______,_________);
坐标为(_______,_________);
(3)画出三角形![]() ,并求其面积。
,并求其面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函双y=![]() (m≠0)的阳象交于点c(n,3),与x轴、y轴分别交于点A、B,过点C作CM⊥x轴,垂足为M,若tan∠CAM=
(m≠0)的阳象交于点c(n,3),与x轴、y轴分别交于点A、B,过点C作CM⊥x轴,垂足为M,若tan∠CAM=![]() ,OA=2.
,OA=2.
(1)求反比例函数和一次函数的解析式;
(2)点D是反比例函数图象在第三象限部分上的一点,且到x轴的距离是3,连接AD、BD,求△ABD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平面直角坐标系中,A(a,0)、B(0,b),且|a+2|+(b+2a)2=0,点P为x轴上一动点,连接BP,在第一象限内作BC⊥AB且BC=AB
(1) 求点A、B的坐标
(2) 如图1,连接CP.当CP⊥BC时,作CD⊥BP于点D,求线段CD的长度
(3) 如图2,在第一象限内作BQ⊥BP且BQ=BP,连接PQ.设P(p,0),直接写出S△PCQ=_____

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com