
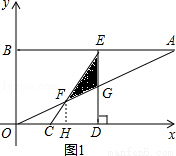
如图,在平面直角坐标系xOy中,点A、B坐标分别为(4,2)、(0,2),线段CD在于x轴上,CD= ,点C从原点出发沿x轴正方向以每秒1个单位长度向右平移,点D随着点C同时同速同方向运动,过点D作x轴的垂线交线段AB于点E、交OA于点G,连结CE交OA于点F.设运动时间为t,当E点到达A点时,停止所有运动.
,点C从原点出发沿x轴正方向以每秒1个单位长度向右平移,点D随着点C同时同速同方向运动,过点D作x轴的垂线交线段AB于点E、交OA于点G,连结CE交OA于点F.设运动时间为t,当E点到达A点时,停止所有运动.

(1)求线段CE的长;
(2)记S为RtΔCDE与ΔABO的重叠部分面积,试写出S关于t的函数关系式及t的取值范围;
(3)连结DF,
①当t取何值时,有 ?
?
②直接写出ΔCDF的外接圆与OA相切时t的值.
(1)线段CE的长为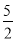 ;
;
(2)S=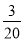 (
(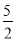 ﹣t)2,t的取值范围为:0≤t≤
﹣t)2,t的取值范围为:0≤t≤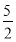 ;
;
(3)①当t=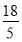 时,DF=CD;②ΔCDF的外接圆与OA相切时t=
时,DF=CD;②ΔCDF的外接圆与OA相切时t=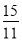 .
.
【解析】
试题分析:(1)直接根据勾股定理求出CE的长即可;
(2)作FH⊥CD于H.,由AB∥OD,DE⊥OD,OB⊥OD可知四边形ODEB是矩形,故可用t表示出AE及BE的长,由相似三角形的判定定理可得出△OCF∽△AEF,△ODG∽△AEG,由相似三角形的性质可用t表示出CF及EG的长,FH∥ED可求出HD的长,由三角形的面积公式可求出S与t的关系式;
(3)①由(2)知CF=t,当DF=CD时,作DK⊥CF于K,则CK=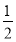 CF=
CF=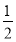 t,CK=CDcos∠DCE,由此可得出t的值;
t,CK=CDcos∠DCE,由此可得出t的值;
②先根据勾股定理求出OA的长,由(2)知HD=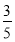 (5﹣t),由相似三角形的判定定理得出Rt△AOB∽Rt△OFH,可用t表示出OF的长,因为当△CDF的外接圆与OA相切时,则OF为切线,OD为割线,由切割线定理可知OF2=OC•OD,故可得出结论.
(5﹣t),由相似三角形的判定定理得出Rt△AOB∽Rt△OFH,可用t表示出OF的长,因为当△CDF的外接圆与OA相切时,则OF为切线,OD为割线,由切割线定理可知OF2=OC•OD,故可得出结论.
试题解析:(1)∵在Rt△CDE中,CD=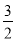 ,DE=2,
,DE=2,
∴CE=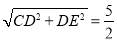 ;
;
(2)如图1,作FH⊥CD于H.
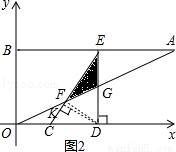
∵AB∥OD,DE⊥OD,OB⊥OD,
∴四边形ODEB是矩形,
∴BE=OD,
∵OC=t,
∴BE=OD=OC+CD=t+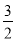 ,
,
∴AE=AB﹣BE=4﹣(t+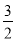 )=
)=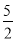 ﹣t,
﹣t,
∵AB∥OD,
∴△OCF∽△AEF,△ODG∽△AEG,
∴ ,
, ,
,
又∵CF+EF=5,DG+EG=4,
∴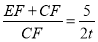 ,
, ,
,
∴CF=t,EG=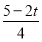 ,
,
∴EF=CE﹣CF=5﹣t,
∵FH∥ED,
∴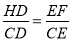 ,即HD=
,即HD=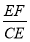 •CD=
•CD=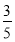 (
(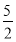 ﹣t),
﹣t),
∴S=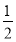 EG•HD=
EG•HD=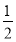 ×
×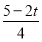 ×
×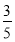 (
(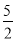 ﹣t)=
﹣t)=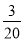 (
(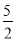 ﹣t)2,
﹣t)2,
t的取值范围为:0≤t≤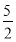 ;
;
(3)①由(2)知CF=t,
如图2,当DF=CD时,如图作DK⊥CF于K,
则CK=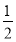 CF=
CF=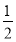 t,
t,
∵CK=CDcos∠DCE,
∴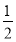 t=3×
t=3×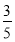 ,
,
解得:t=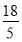 ;
;
∴当t=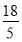 时,DF=CD;
时,DF=CD;
②∵点A,B坐标分别为(8,4),(0,4),
∴AB=8,OB=4,
∴OA= =4
=4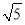 ,
,
∵由(2)知HD=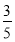 (5﹣t),
(5﹣t),
∴OH=t+3﹣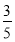 (5﹣t)=
(5﹣t)=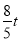 ,
,
∵∠A+∠AOB=∠AOD+∠AOB=90°,
∴∠A=∠AOD,
∴Rt△AOB∽Rt△OFH,
∴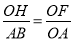 ,
,
解得OF=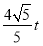 ,
,
∵当△CDF的外接圆与OA相切时,则OF为切线,OD为割线,
∴OF2=OC•OD,即(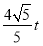 )2=t(t+3),得t=
)2=t(t+3),得t=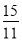 .
.
考点:相似形综合题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2013-2014学年江苏省南京市六合区中考一模数学试卷(解析版) 题型:解答题
如图,四边形ABCD为矩形,四边形AEDF为菱形.
(1)求证:△ABE≌△DCE;
(2)试探究:当矩形ABCD边长满足什么关系时,菱形AEDF为正方形?请说明理由.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省兴化市九年级中考网上阅卷适应性训练(即一模)数学试卷(解析版) 题型:选择题
两个大小不同的球在水平面上靠在一起,组成如图所示的几何体,则该几何体的左视图是( )

A.两个外离的圆 B.两个外切的圆
C.两个相交的圆 D.两个内切的圆
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省兴化市九年级中考网上阅卷适应性训练(二模)数学试卷(解析版) 题型:填空题
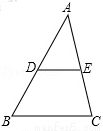
如图,在△ABC中,点D,E分别是AB,AC的中点,∠A=50°,∠ADE=60°,则∠C= .
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省兴化市九年级中考网上阅卷适应性训练(二模)数学试卷(解析版) 题型:选择题
兴化市教育局为帮助全市贫困师生举行“一日捐”活动,甲、乙两校教师各捐款30000元,已知“…”,设乙学校教师有x人,则可得方程 ,根据此情景,题中用“…”表示的缺失的条件应补( )
,根据此情景,题中用“…”表示的缺失的条件应补( )
A.乙校教师比甲校教师人均多捐20元,且甲校教师的人数比乙校教师的人数多20%
B.甲校教师比乙校教师人均多捐20元,且乙校教师的人数比甲校教师的人数多20%
C.甲校教师比乙校教师人均多捐20元,且甲校教师的人数比乙校教师的人数多20%
D.乙校教师比甲校教师人均多捐20元,且乙校教师的人数比甲校教师的人数多20%
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏大丰刘庄第二初中九年级下学期第一次月考数学试卷(解析版) 题型:解答题
某地区冬季干旱,康平社区每天需从外地调运饮用水60吨.有关部门紧急部署,从甲、乙两水厂调运饮用水到供水点,甲厂每天最多可调出40吨,乙厂每天最多可调出45吨.从两水厂运水到康平社区供水点的路程和运费如下表:
| 到康平社区供水点的路程(千米) | 运费(元/吨·千米) |
甲厂 | 20 | 4 |
乙厂 | 14 | 5 |
(1)若某天调运水的总运费为4450元,则从甲、乙两水厂各调运了多少吨饮用水?
(2)设从甲厂调运饮用水x吨,总运费为W元,试写出W关于x的函数关系式,并确定x的取值范围.怎样安排调运方案才能使每天的总运费最省?
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏大丰刘庄第二初中九年级下学期第一次月考数学试卷(解析版) 题型:填空题
如图,将△ABC沿直线AB向右平移后到达△BDE的位置,若∠CAB=50°,∠ABC=100°,则∠CBE的度数为 .

查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏仪征大仪中学九年级3月月考数学试卷(解析版) 题型:解答题
如图,梯形ABCD中,AB∥CD,∠ABC=90°,AB=8,CD=6,BC=4,AB边上有一动点P(不与A、B重合),连结DP,作PQ⊥DP,使得PQ交射线BC于点E,设AP=x.



⑴当x为何值时,△APD是等腰三角形?
⑵若设BE=y,求y关于x的函数关系式;
⑶若BC的长可以变化,在现在的条件下,是否存在点P,使得PQ经过点C?若存在,求出相应的AP的长;若不存在,请说明理由,并直接写出当BC的长在什么范围内时,可以存在这样的点P,使得PQ经过点C.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com