Question

如图，梯形ABCD中，AB∥CD，∠ABC=90°，AB=8，CD=6，BC=4，AB边上有一动点P(不与A、B重合)，连结DP，作PQ⊥DP，使得PQ交射线BC于点E，设AP=x．

⑴当x为何值时，△APD是等腰三角形?

⑵若设BE=y，求y关于x的函数关系式；

⑶若BC的长可以变化，在现在的条件下，是否存在点P，使得PQ经过点C?若存在，求出相应的AP的长；若不存在，请说明理由，并直接写出当BC的长在什么范围内时，可以存在这样的点P，使得PQ经过点C．

 

Answer 1

．

【解析】

试题分析：（1）过D点作DH⊥AB于H，则四边形DHBC为矩形，在Rt△AHD中，由勾股定理可求得DH、AD、PH的值，若△ADP为等腰三角形，则分三种情况：①当AP=AD时，x=AP=AD，②当AD=PD时，有AH=PH，故x=AH+PH，③当AP=PD时，则在Rt△DPH中，由勾股定理可求得DP的值，有x=AP=DP．

（2）易证：△DPH∽△PEB?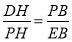，即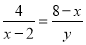，故可求得y与x的关系式．

（3）利用△DPH∽△PEB，得出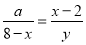，进而利用根的判别式和一元二次不等式解集得出即可．

试题解析：（1）过D点作DH⊥AB于H，则四边形DHBC为矩形，

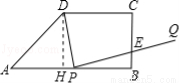
∴DH=BC=4，HB=CD=6．

∴AH=2，AD=2．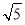

∵AP=x，

∴PH=x﹣2，

情况①：当AP=AD时，即x=2．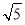

情况②：当AD=PD时，则AH=PH．

∴2=x﹣2，解得x=4．

情况③：当AP=PD时，

则Rt△DPH中，x2=42+（x﹣2）2，解得x=5．

∵2＜x＜8，

∴当x为2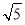、4、5时，△APD是等腰三角形．

（2）∵∠DPE=∠DHP=90°，

∴∠DPH+∠EPB=∠DPH+∠HDP=90°．

∴∠HDP=∠EPB．

又∵∠DHP=∠B=90°，

∴△DPH∽△PEB．

∴，

∴．

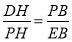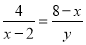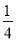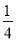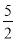整理得：y=（x﹣2）（8﹣x）=﹣x2+x﹣4；

（3）存在．

设BC=a，则由（2）得△DPH∽△PEB，

∴，

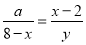∴y=，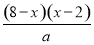

当y=a时，

（8﹣x）（x﹣2）=a2

x2﹣10x+（16+a2）=0，

∴△=100﹣4（16+a2），

∵△≥0，

∴100﹣64﹣4a2≥0，

4a2≤36，

又∵a＞0，

∴a≤3，

∴0＜a≤3，

∴满足0＜BC≤3时，存在点P，使得PQ经过C．

考点：1.一元二次方程2.相似三角形的判定与性质．