
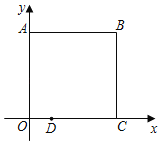
【题目】在平面直角坐标系中,A(0,4)、B(4,4)、C(4,0),D(1,0).
(1)若抛物线经过A、B、D三点,求此抛物线的解析式;
(2)若(1)中的抛物线的顶点为E,连接EB,若P是EB上一动点,过P点作PM⊥AB,PN垂直于y轴,垂足分别是M、N.求矩形AMPN面积的最大值.
【答案】(1)y=![]() x2
x2![]() x+4;(2)最大值为
x+4;(2)最大值为![]() .
.
【解析】
(1)设抛物线的解析式为:y=ax2+bx+c,把A(0,4)、B(4,4)、D(1,0)代入y=ax2+bx+c列方程组即可得到结论;
(2)由(1)可知,抛物线的顶点坐标E(2,-![]() ),求得直线BE的解析式为y=
),求得直线BE的解析式为y=![]() x-
x-![]() ,设P点的坐标为(m,
,设P点的坐标为(m,![]() m-
m-![]() ),根据二次函数的性质即可得到结论.
),根据二次函数的性质即可得到结论.
解:(1)设抛物线的解析式为:y=ax2+bx+c,
把A(0,4)、B(4,4)、D(1,0)代入y=ax2+bx+c得,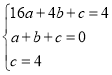 ,
,
解得: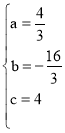 ,
,
∴抛物线的解析式为:y=![]() x2
x2![]() x+4;;
x+4;;
(2)如图,
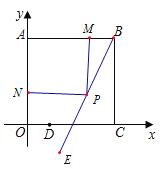
由(1)可知,抛物线的顶点坐标E(2,﹣![]() ),
),
设直线BE的解析式为:y=kx+b,把B为(4,4),E(2,﹣![]() )代入得
)代入得
 ,
,
∴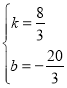 ,
,
∴直线BE的解析式为y=![]() x﹣
x﹣![]() ,
,
∴设P点的坐标为(m,![]() m﹣
m﹣![]() ),
),
∴S矩形AMPN=[4﹣(![]() m﹣
m﹣![]() )]m﹣﹣
)]m﹣﹣![]() m2+
m2+![]() m=﹣
m=﹣![]() (m﹣2)2+
(m﹣2)2+![]() ,
,
∴当m=2时,矩形AMPN面积的最大值为![]() .
.


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案科目:初中数学 来源: 题型:
【题目】新能源汽车投放市场后,有效改善了城市空气质量。经过市场调查得知,某市去年新能源汽车总量已达到3250辆,预计明年会增长到6370辆.
(1)求今、明两年新能源汽车数量的平均增长率;
(2)为鼓励市民购买新能源汽车,该市财政部门决定对今年增加的新能源汽车给予每辆0.8万元的政府性补贴.在(1)的条件下,求该市财政部门今年需要准备多少补贴资金?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,矩形ABCD的位置如图1所示,点A的坐标为(-2,0),点B的坐标为(0,2),点D的坐标为(-3,1).矩形ABCD以每秒1个单位长度的速度沿x轴正方向运动,设运动时间为x(0≤x≤3)秒,第一象限内的图形面积为y,则下列图象中表示y与x的函数关系的图象大致是
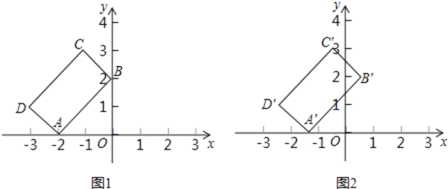
A. 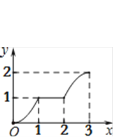 B.
B. 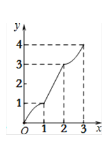 C.
C. 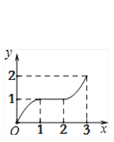 D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c的自变量x与函数值y的对应值如图,下列说法错误的是:( )
x | … | ﹣6 | ﹣5 | ﹣4 | ﹣3 | ﹣2 | ﹣1 | … |
y | … | 10 | 4 | 0 | ﹣2 | ﹣2 | 0 | … |
A.抛物线开口向上
B.抛物线与y轴的交点是(0,4)
C.当x<﹣2时,y随x的增大而减小
D.当x>﹣2时,y随x的增大而增大
查看答案和解析>>
科目:初中数学 来源: 题型:
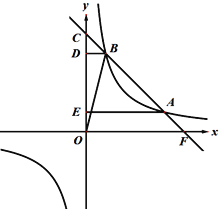
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() (
(![]() )的图象在第一象限交于点A,B,且该一次函数的图象与y轴正半轴交于点C,过A,B分别作y轴的垂线,垂足分别为E,D,且
)的图象在第一象限交于点A,B,且该一次函数的图象与y轴正半轴交于点C,过A,B分别作y轴的垂线,垂足分别为E,D,且![]() .已知A(m,1),AE=4BD.
.已知A(m,1),AE=4BD.
(1)填空:m= ;k= ;
(2)求B点的坐标和一次函数的解析式;
(3)将直线AB向下平移m(m>0)个单位,使它与反比例函数图象有唯一交点,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
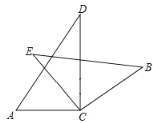
【题目】两块不同的三角板按如图所示摆放,两个直角顶点C重合,![]() ,
,![]() 。接着保持三角板ACD不动,将三角板CBE绕着点C旋转,但保证点E在直线AC的上方,若三角板CBE有一条边与斜边AD平行,则∠ACE=__________.
。接着保持三角板ACD不动,将三角板CBE绕着点C旋转,但保证点E在直线AC的上方,若三角板CBE有一条边与斜边AD平行,则∠ACE=__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年是我市脱贫攻坚决战决胜的关键之年,阳高灵丘、云州三县区要在今年实现脱贫摘帽.近年来,享有“中国黄花之乡的云州区坚持把产业扶贫作为扶贫攻坚的重要支撑,黄花销售也成为区政府关注的一项民生工程.现有成本为每千克80元的大同特级黄花菜干货,经市场分析,若按每千克100元销售,一个月能售出800千克;销售单价每涨价1元,月销售量就减少10千克.针对黄花菜的销售情况,请解答以下问题.
(1)现计划在月销售成本不超过40000元的情况下,使得月销售利润达到24000元,销售单价应定为多少元?
(2)定价为多少元时,农民销售可获得最大利润?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com