
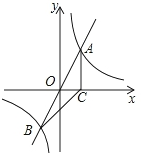
 如图,正比例函数y=2x的图象与反比例函数y=$\frac{k}{x}$的图象交于A、B两点,过点A作AC垂直x轴于点C,连结BC.若△ABC的面积为2.
如图,正比例函数y=2x的图象与反比例函数y=$\frac{k}{x}$的图象交于A、B两点,过点A作AC垂直x轴于点C,连结BC.若△ABC的面积为2.分析 (1)根据对称性可得OA=OB,从而可得△ACO的面积为1,由此可求出点A的坐标,然后运用待定系数法就可解决问题;
(2)只需求出点B的坐标,并运用数形结合的思想就可解决问题.
解答 解:(1)设点A的坐标为(m,n).
∵点A在直线y=2x上,∴n=2m.
根据对称性可得OA=OB,
∴S△ABC=2S△ACO=2,
∴S△ACO=1,
∴$\frac{1}{2}$m•2m=1,
∴m=1(舍负),
∴点A的坐标为(1,2),
∴k=1×2=2;
(2)如图,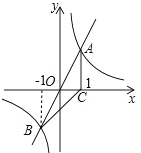
由点A与点B关于点O成中心对称得点B(-1,-2).
结合图象可得:不等式2x>$\frac{k}{x}$的解集为x>1或-1<x<0.
点评 本题主要考查了中心对称的性质、运用待定系数法求出反比例函数的解析式,运用数形结合的思想是解决第(2)小题的关键.


科目:初中数学 来源: 题型:选择题
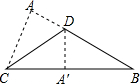 如图,将一张△ABC的纸片沿CD进行折叠,点A的对应点A′恰好落在BC上,CA′:A′B=3:2.若△ABC的面积为96,则△ACD的面积为( )
如图,将一张△ABC的纸片沿CD进行折叠,点A的对应点A′恰好落在BC上,CA′:A′B=3:2.若△ABC的面积为96,则△ACD的面积为( )| A. | 34 | B. | 30 | C. | 36 | D. | 56 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 高铁和特快两列火车分别从相距1000千米路程的甲、乙两地同时出发,先相向而行,高铁到达乙地后,停留1小时,然后按原路原速返回,高铁比特快晚1小时到达甲地,高铁和特快两列火车距甲地的路程y(千米)与出发后所用的时间x(小时)的关系如图所示,假定这两列火车均匀速行驶.
高铁和特快两列火车分别从相距1000千米路程的甲、乙两地同时出发,先相向而行,高铁到达乙地后,停留1小时,然后按原路原速返回,高铁比特快晚1小时到达甲地,高铁和特快两列火车距甲地的路程y(千米)与出发后所用的时间x(小时)的关系如图所示,假定这两列火车均匀速行驶.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
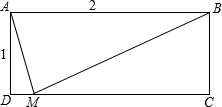 矩形ABCD中,AB=2,AD=1,点M在边CD上,若AM平分∠DMB,则DM的长是( )
矩形ABCD中,AB=2,AD=1,点M在边CD上,若AM平分∠DMB,则DM的长是( )| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{1}{4}$ | C. | $\sqrt{3}-\frac{3}{2}$ | D. | $2-\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
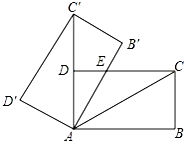 如图,将矩形ABCD绕点A旋转至矩形AB′C′D′位置,此时AC的中点恰好与D点重合,AB′交CD于点E.若AB=6,则△AEC的面积为( )
如图,将矩形ABCD绕点A旋转至矩形AB′C′D′位置,此时AC的中点恰好与D点重合,AB′交CD于点E.若AB=6,则△AEC的面积为( )| A. | 12 | B. | 4$\sqrt{3}$ | C. | 8$\sqrt{3}$ | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m=2,n=-3 | B. | m=-2,n=3 | C. | m=-2,n=-3 | D. | m=2,n=3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
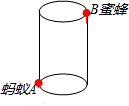 如图,圆柱形容器高12cm,底面周长24cm,在杯口点B处有一滴蜂蜜,此时蚂蚁在杯外壁底部与蜂蜜相对的A处,
如图,圆柱形容器高12cm,底面周长24cm,在杯口点B处有一滴蜂蜜,此时蚂蚁在杯外壁底部与蜂蜜相对的A处,查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com