若代数式x2-6x+m可化为(x-n)2-1.则m-n= ．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

若代数式x²-6x+m可化为（x-n）²-1，则m-n=

．

考点：配方法的应用

专题：

分析：代数式配方后，根据多项式相等的条件求出m与n的值，即可求出m-n的值．

解答：解：代数式x²-6x+m=x²-6x+9-9+m=（x-3）²-9+m=（x-n）²-1，
∴n=3，-9+m=-1，即m=8，
则m-n=8-3=5．
故答案为：5．

点评：此题考查了配方法的应用，熟练掌握完全平方公式是解本题的关键．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

先化简，再求值：（

2x2+2x

x2-1

x-1

）÷

x+1

，其中x=（

）^-1-（π-1）⁰+

．

查看答案和解析>>

科目：初中数学 来源： 题型：

如图，对称轴为直线x=2的抛物线经过A（-1，0），C（0，5）两点，与x轴另一交点为B．已知M（0，1），E（a，0），F（a+1，0），点P是第一象限内的抛物线上的动点．
（1）求此抛物线的解析式；
（2）当a=1时，求四边形MEFP的面积的最大值，并求此时点P的坐标；
（3）若△PCM是以点P为顶点的等腰三角形，求a为何值时，四边形PMEF周长最小？请说明理由．

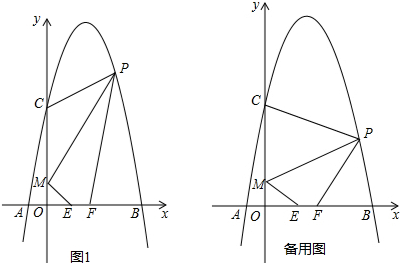
查看答案和解析>>

科目：初中数学 来源： 题型：

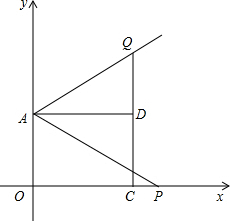如图，在矩形AOCD中，AO=3，0C=4，以AO，OC，所在直线为x轴，y轴建立直角坐标系，点P是OC延长线上一点，把射线AP沿直线AD翻折，交射线CD于点Q．
（1）若CP=1，求直线PQ的解析式；
（2）设点P的坐标为（m，0），△APQ的面积等于12，求m的值或m的取值范围；
（3）在（1）的条件下，将△AOC以每秒1个单位的速度沿x轴正方向运动，直到O与P重合时停止．设运动的时间为t，△OAC移动后的三角形为O′A′C′，若△O′A′C′与△APD重叠部分的面积为S，请求出S与t的函数关系式．

查看答案和解析>>

科目：初中数学 来源： 题型：

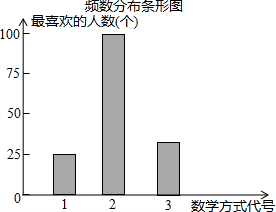某中学为促进课堂教学，提高教学质量，对七年级学生进行了一次“你最喜欢的课堂教学方式”的问卷调查．根据收回的问卷，学校绘制了“频数分布表”和“频数分布条形图”．请你根据图表中提供的信息，解答下列问题．
频数分布表

代号	教学方式	最喜欢的频数	频率
1	老师讲，学生听	20	0.10
2	老师提出问题，学生探索思考	100	a
3	学生自行阅读教材，独立思考	30	0.15
4	分组讨论，解决问题	b	0.25