
【题目】景新中学为了进一步丰富学生的课外阅读,欲增购一些课外书,为此对该校一部分学生进行了一次“你最喜欢的书籍”问卷调查(每人只选一项).根据收集到的数据,绘制成如下统计图(不完整):请根据图中提供的信息,完成下列问题: 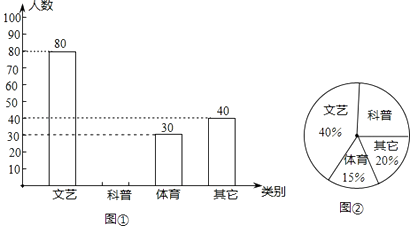
(1)在这次问卷调查中,喜欢“科普书籍”出现的频率为;
(2)在扇形统计图中,喜欢“体育书籍”的所占的圆心角度数为;
(3)如果全校共有学生1500名,请估计该校最喜欢“科普书籍”的学生约有人.
【答案】
(1)0.25
(2)54°
(3)375
【解析】解:(1)在这次问卷调查中,喜欢“科普书籍”出现的频率为1﹣20%﹣15%﹣40%=25%=0.25. ·(2)喜欢“体育书籍”的所占的圆心角度数15%×360°=54°.
·(3)估计该校最喜欢“科普”书籍的学生数为1500×25%=375名.
所以答案是:(1)0.25;(2)54°;(3)375.
【考点精析】通过灵活运用扇形统计图和条形统计图,掌握能清楚地表示出各部分在总体中所占的百分比.但是不能清楚地表示出每个项目的具体数目以及事物的变化情况;能清楚地表示出每个项目的具体数目,但是不能清楚地表示出各个部分在总体中所占的百分比以及事物的变化情况即可以解答此题.


 高效智能课时作业系列答案
高效智能课时作业系列答案科目:初中数学 来源: 题型:
【题目】老师在黑板上出了一道解方程的题![]() ,小虎马上举手,要求到黑板上去做,他是这样做的:
,小虎马上举手,要求到黑板上去做,他是这样做的:
5(3x-1)=2(4x+2)-1①,
15x-5=8x+4-1②,
15x-8x=4-1+5③
7x④,
x=![]() ⑤
⑤
老师说:小虎解一元一次方程的一般步骤都知道,但没有掌握好,因此解题出现了错误,请指出他的错步及错误原因: ,方程的正确的解是x= .
然后,你自己细心的解下面的方程:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,扇形AOB中,OA=10,∠AOB=36°.若将此扇形绕点B顺时针旋转,得一新扇形A′O′B,其中A点在O′B上,则点O的运动路径长为cm.(结果保留π) 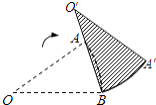
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图的抛物线是把抛物线y= ![]() x2平移后经过(0,﹣1)和(4,﹣1)两点得到的.
x2平移后经过(0,﹣1)和(4,﹣1)两点得到的. 
(1)求平移后抛物线的表达式.
(2)求平移后方向和距离.
(3)在平移后的抛物线上取一点P,以P为圆心作半径为2的⊙P,当⊙P与y轴相切时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D为AB边上一点.
(1)求证:AD2+DB2=ED2;
(2)若BC=![]() ,求四边形ADCE的面积.
,求四边形ADCE的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年2月18日韩国海军海警在朝鲜半岛东部海域实施联合演习,在返回济州岛军事基地途中,韩国海军UH﹣60直升机在距海平面垂直高度为300米的点C处测得济州一小岛的西端点A的俯角为60°,然后沿着平行于AB的方向水平飞行了3500米,在点D测得这小岛的东端点B的俯角为45°,求这个济州小岛东西两端BA的距离(结果精确到1米,参考数据: ![]() ≈1.732,
≈1.732, ![]() ≈1.414)
≈1.414)
查看答案和解析>>
科目:初中数学 来源: 题型:
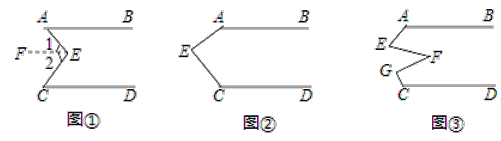
【题目】(感知)如图①,AB∥CD,点E在直线AB与CD之间,连结AE、BE,试说明∠BEE+∠DCE=∠AEC.下面给出了这道题的解题过程,请完成下面的解题过程,并填空(理由或数学式):
解:如图①,过点E作EF∥AB
∴∠BAE=∠1( )
∵AB∥CD( )
∴CD∥EF( )
∴∠2=∠DCE
∴∠BAE+∠DCE=∠1+∠2( )
∴∠BAE+∠DCE=∠AEC
(探究)当点E在如图②的位置时,其他条件不变,试说明∠AEC+∠FGC+∠DCE=360°;
(应用)点E、F、G在直线AB与CD之间,连结AE、EF、FG和CG,其他条件不变,如图③.若∠EFG=36°,则∠BAE+∠AEF+∠FGC+∠DCG= °.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某同学做一道数学题,已知两个多项式A、B,B=3x2y-5xy+x+7,试求A+B,这位同学把A+B看成A-B,结果求出的答案为6x2y+12xy-2x-9.
(1)请你替这位同学求出的正确答案;
(2)当x取任意数值,A-3B的值是一个定值,求y的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com