
【题目】如图,△ACB和△ECD都是等腰直角三角形,∠ACB=∠ECD=90°,点D为AB边上一点.
(1)求证:AD2+DB2=ED2;
(2)若BC=![]() ,求四边形ADCE的面积.
,求四边形ADCE的面积.

【答案】(1)见解析;(2)1.
【解析】
(1)先证明△ACE≌△BCD,即可得到AE=BD,∠CAE=∠B=45°,再根据∠DAE=90°,即可得出AD2+DB2=ED2;(2)依据△ACE≌△BCD,可得S△ACE=S△BCD,即可得到S四边形ADCE=S△ABC,由此即可求解.
解:(1)∵△ACB和△ECD都是等腰直角三角形,
∴∠ACB=∠ECD=90°,EC=CD,AC=CB,
∴∠ECA=∠DCB
在△ECA和△DCB中,
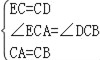 ,
,
∴△ACE≌△BCD(SAS),
∴AE=BD,∠CAE=∠B=45°,
∴∠DAE=90°,
∴AD2+AE2=ED2即AD2+DB2=ED2.
(2)∵△ACE≌△BCD,
∴S△ACE=S△BCD,
∴S四边形ADCE=S△ABC=![]() ×(
×(![]() )2=1.
)2=1.


 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案科目:初中数学 来源: 题型:
【题目】计算
(1)8﹣(﹣2)
(2)1﹣6+(﹣20)﹣(﹣5)
(3)﹣4×(﹣3)2+5×(﹣2)﹣6
(4)(1﹣![]() +
+![]() )×(﹣48)
)×(﹣48)
(5)﹣22+[(﹣4)2﹣(1﹣3)×3]
(6)(﹣125![]() )÷(﹣5)
)÷(﹣5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四个全等的直角三角形纸片既可以拼成(内角不是直角)的菱形ABCD,也可以拼成正方形EFGH,则菱形ABCD面积和正方形EFGH面积之比为( ) 
A.1
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AE切⊙O于点E,AT交⊙O于点M,N,线段OE交AT于点C,OB⊥AT于点B,已知∠EAT=30°,AE=3 ![]() ,MN=2
,MN=2 ![]() .
. 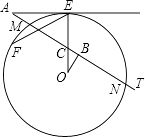
(1)求∠COB的度数;
(2)求⊙O的半径R;
(3)点F在⊙O上( ![]() 是劣弧),且EF=5,把△OBC经过平移、旋转和相似变换后,使它的两个顶点分别与点E,F重合.在EF的同一侧,这样的三角形共有多少个?你能在其中找出另一个顶点在⊙O上的三角形吗?请在图中画出这个三角形,并求出这个三角形与△OBC的周长之比.
是劣弧),且EF=5,把△OBC经过平移、旋转和相似变换后,使它的两个顶点分别与点E,F重合.在EF的同一侧,这样的三角形共有多少个?你能在其中找出另一个顶点在⊙O上的三角形吗?请在图中画出这个三角形,并求出这个三角形与△OBC的周长之比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】景新中学为了进一步丰富学生的课外阅读,欲增购一些课外书,为此对该校一部分学生进行了一次“你最喜欢的书籍”问卷调查(每人只选一项).根据收集到的数据,绘制成如下统计图(不完整):请根据图中提供的信息,完成下列问题: 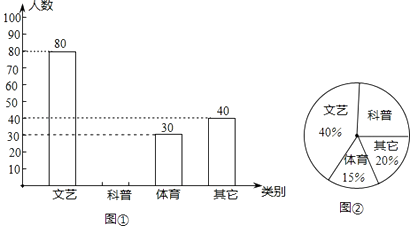
(1)在这次问卷调查中,喜欢“科普书籍”出现的频率为;
(2)在扇形统计图中,喜欢“体育书籍”的所占的圆心角度数为;
(3)如果全校共有学生1500名,请估计该校最喜欢“科普书籍”的学生约有人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:直线y=﹣x﹣4分别交x、y轴于A、C两点,抛物线y=ax2+bx(a>0)经过A、O两点,且顶点B的纵坐标为﹣2 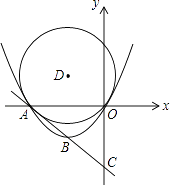
(1)判断点B是否在直线AC上,并求该抛物线的函数关系式;
(2)以点B关于x轴的对称点D为圆心,以OD为半径作⊙D,试判断直线AC与⊙D的位置关系,并说明理由;
(3)若E为⊙D的优弧AO上一动点(不与A、O重合),连结AE、OE,问在抛物线上是否存在点P,使∠POA:∠AEO=2:3?若存在,请求出所有满足条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AC是切⊙O于A的切线,BC交⊙O于点D,E是劣弧 ![]() 的中点,连接AE交BC于点F,若cosC=
的中点,连接AE交BC于点F,若cosC= ![]() ,AC=6,则BF的长为 .
,AC=6,则BF的长为 . 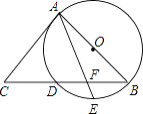
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某玩具厂熟练工人工资为:每月底薪700元,加奖励工资按件计算,一个月工作日为25天,每天工作8小时,加工1件A种玩具计酬10元,加工1件B种玩具计酬8元.在工作中发现一名熟练工人加工1件A种玩具和2件B种玩具需4小时,加工3件A种玩具和1件B种玩具需7小时.(工人月工资=底薪+计件工资)
(1)求熟练工人每加工一件A种玩具和一件B种玩具,分别需要多少时间?
(2)深圳市规定最低工资标准为每月2030元,但玩具厂规定:“每名工人每月必须加工A、B两种工具,且加工A种玩具数量不少于B种玩具的一半”.若设一名熟练工人每月加工A种玩具a件,工资总额为w元,请你运用所学知识判断该公司在执行规定后是否违背了深圳市最低工资标准?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com