Question

【题目】如图，在边长为 2 的正方形 ABCD 中，点 P 、Q 分别是边 AB 、 BC 上的两个动点（与点 A 、B 、C 不重合）且始终保持 BP BQ, AQ QE ，QE 交正方形外角平分线CE 于点 E ， AE 交CD 于点 F ，连结 PQ 。

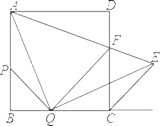
（1）求证： APQ ≌ QCE ；

（2）求QAE 的度数；

（3）设 BQ x ，当 x 为何值时， QF CE ，并求出此时AQF 的面积。

Answer 1

【答案】(1)见解析;(2)45°;(3) 2-2；4-4.

【解析】

（1）判断出△PBQ是等腰直角三角形,然后求出∠APQ=∠QCE=135°,再根据同角的余角相等求出∠PAQ=∠CQE,再求出AP=CQ,然后利用“角边角”证明即可;（2）根据全等三角形对应边相等可得AQ=EQ,判断出△AQE是等腰直角三角形,再根据等腰直角三角形的性质解答; （3）把△ABQ绕点A逆时针旋转90°得到△ADG,求出∠GAF=45°,从而得到∠GAF=∠QAF,再利用“边角边”证明△AQF和△AGF全等,根据全等三角形对应边相等可得QF=GF,再根据两直线平行,同位角相等求出∠CQF=45°,然求出CQ=CF,分别用x表示出CQ、CF、QF,利用勾股定理列式表示出QF,然后列出方程求出x,再求出△AGF的面积,即为△AQF的面积．

（1）证明：在正方形ABCD中,∠B=90°,AB=BC,∵BP=BQ,

∴△PBQ是等腰直角三角形,AP=CQ,

∴∠BPQ=45°,

∵CE为正方形外角的平分线,

∴∠APQ=∠QCE=135°,

∵AQ⊥QE,

∴∠CQE+∠AQB=90°,

又∵∠PAQ+∠AQB=90°,

∴∠PAQ=∠CQE,

在△APQ和△QCE中,

,

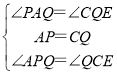∴△APQ≌△QCE（ASA）;

（2）解：∵△APQ≌△QCE,

∴AQ=EQ,

∵AQ⊥QE,

∴△AQE是等腰直角三角形,

∴∠QAE=45°;

（3）解：如图，把△ABQ绕点A逆时针旋转90°得到△ADG,

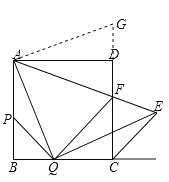
则AQ=AG,BQ=DG,∠BAQ==∠DAG,

∵∠QAE=45°,

∴∠GAF=45°,∠GAF=∠QAF,

在△AQF和△AGF中,

,

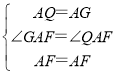∴△AQF≌△AGF（SAS）,

∴QF=GF,

∵QF∥CE,

∴∠CQF=45°,

∴△CQF是等腰直角三角形,

∴CQ=CF,

∵BQ=x,

∴CQ=CF=2-x,

∴DF=2-（2-x）=x,

∴QF=GF=2x,

在Rt△CQF中,CQ2+CF2=QF2, 即（2-x）2+（2-x）2=（2x）2,

解得x=2-2,

∴△AGF的面积=×2（2-2）×2=4-4， 即△AQF的面积为4-4．