
【题目】如图,四边形ABCD中,∠A=∠C=90°,∠ABC=135°,CD=6,AB=2,则四边形ABCD的面积为___________

【答案】16
【解析】
延长AB和DC,两线交于O,求出OB=![]() BC,OD=
BC,OD=![]() OA,OA=AD,BC=OC,设BC=OC=x,则BO=
OA,OA=AD,BC=OC,设BC=OC=x,则BO=![]() x,解直角三角形得出方程,求出x,再分别求出△AOD和△BOC的面积即可.
x,解直角三角形得出方程,求出x,再分别求出△AOD和△BOC的面积即可.
延长AB和DC,两线交于O,
∵∠C=90°,∠ABC=135°,
∴∠OBC=45°,∠BCO=90°,
∴∠O=45°,
∵∠A=90°,
∴∠D=45°,
则OB=![]() BC,OD=
BC,OD=![]() OA,OA=AD,BC=OC,
OA,OA=AD,BC=OC,
设BC=OC=x,则BO=![]() x,
x,
∵CD=6,AB=2,
∴6+x=![]() (
(![]() x+2),
x+2),
解得:x=6-2![]() ,
,
∴OB=6![]() -4,BC=OC=6-2
-4,BC=OC=6-2![]() ,OA=AD=2+6
,OA=AD=2+6![]() -4=6
-4=6![]() -2,
-2,
∴S四边形ABCD=S△OAD-S△OBC
=![]() OAAD-
OAAD-![]() BCOC
BCOC
=![]()
=16,
故答案为:16.


科目:初中数学 来源: 题型:
【题目】如图,在边长为 2 的正方形 ABCD 中,点 P 、Q 分别是边 AB 、 BC 上的两个动点(与点 A 、B 、C 不重合)且始终保持 BP BQ, AQ QE ,QE 交正方形外角平分线CE 于点 E , AE 交CD 于点 F ,连结 PQ 。
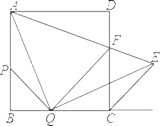
(1)求证: APQ ≌ QCE ;
(2)求QAE 的度数;
(3)设 BQ x ,当 x 为何值时, QF CE ,并求出此时AQF 的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
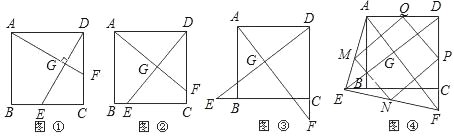
【题目】如图1,在正方形ABCD中,点E、F分别为边BC、CD的中点,AF、DE相交于点G,则可得结论:①AF=DE,②AF⊥DE(不须证明).
(1)如图②,若点E、F不是正方形ABCD的边BC、CD的中点,但满足CE=DF,则上面的结论①、②是否仍然成立;(请直接回答“成立”或“不成立”)
(2)如图③,若点E、F分别在正方形ABCD的边CB的延长线和DC的延长线上,且CE=DF,此时上面的结论①、②是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由.
(3)如图④,在(2)的基础上,连接AE和EF,若点M、N、P、Q分别为AE、EF、FD、AD的中点,请先判断四边形MNPQ是“矩形、菱形、正方形、等腰梯形”中的哪一种,并写出证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
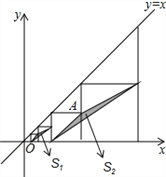
【题目】如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数y=x的图象上,从左向右第3个正方形中的一个顶点A的坐标为(8,4),阴影三角形部分的面积从左向右依次记为S1、S2、S3、…、Sn,则Sn的值为__.(用含n的代数式表示,n为正整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境
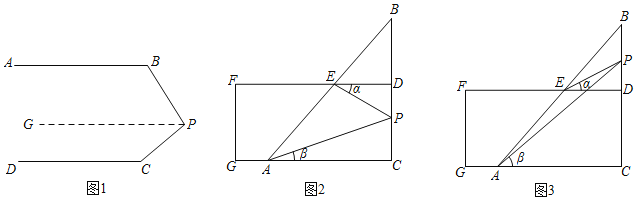
(1)如图1,已知AB∥CD,∠PBA=125°,∠PCD=155°,求∠BPC的度数.
佩佩同学的思路:过点P作PG∥AB,进而PG∥CD,由平行线的性质来求∠BPC,求得∠BPC=
问题迁移
(2)图2.图3均是由一块三角板和一把直尺拼成的图形,三角板的两直角边与直尺的两边重合,∠ACB=90°,DF∥CG,AB与FD相交于点E,有一动点P在边BC上运动,连接PE,PA,记∠PED=∠α,∠PAC=∠β.
①如图2,当点P在C,D两点之间运动时,请直接写出∠APE与∠α,∠β之间的数量关系;
②如图3,当点P在B,D两点之间运动时,∠APE与∠α,∠β之间有何数量关系?请判断并说明理由;
拓展延伸
(3)当点P在C,D两点之间运动时,若∠PED,∠PAC的角平分线EN,AN相交于点N,请直接写出∠ANE与∠α,∠β之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是等边△ABC内一点,D是△ABC外的一点,∠AOB=110°,∠BOC=![]() ,△BOC≌△ADC,∠OCD=60°,连接OD.
,△BOC≌△ADC,∠OCD=60°,连接OD.
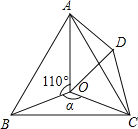
(1)求证:△OCD是等边三角形;
(2)当α=150°时,试求证:△AOD是直角三角形;
(3)△AOD能否为等边三角形?为什么?
(4)探究:当α为多少度时,△AOD是等腰三角形.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,图象过点(﹣1,0),对称轴为直线x=2,下列结论:(1)4a+b=0;(2)9a+c>﹣3b;(3)7a﹣3b+2c>0;(4)若点A(﹣3,y1)、点B(﹣![]() ,y2)、点C(7,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有( )
,y2)、点C(7,y3)在该函数图象上,则y1<y3<y2;(5)若方程a(x+1)(x﹣5)=﹣3的两根为x1和x2,且x1<x2,则x1<﹣1<5<x2.其中正确的结论有( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
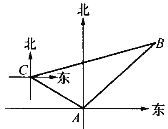
【题目】如图,甲、乙两只捕捞船同时从A港出海捕鱼,甲船以每小时15![]() 千米的速度沿西偏北30°方向前进,乙船以每小时15千米的速度沿东北方向前进,甲船航行2小时到达C处,此时甲船发现渔具丢在乙船上,于是甲船快速(匀速)沿北偏东75°的方向追赶,结果两船在B处相遇.
千米的速度沿西偏北30°方向前进,乙船以每小时15千米的速度沿东北方向前进,甲船航行2小时到达C处,此时甲船发现渔具丢在乙船上,于是甲船快速(匀速)沿北偏东75°的方向追赶,结果两船在B处相遇.
(1)甲船从C处追赶上乙船用了多少时间?
(2)甲船追赶乙船的速度是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com