
【题目】如图,点O是等边△ABC内一点,D是△ABC外的一点,∠AOB=110°,∠BOC=![]() ,△BOC≌△ADC,∠OCD=60°,连接OD.
,△BOC≌△ADC,∠OCD=60°,连接OD.
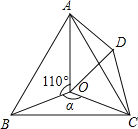
(1)求证:△OCD是等边三角形;
(2)当α=150°时,试求证:△AOD是直角三角形;
(3)△AOD能否为等边三角形?为什么?
(4)探究:当α为多少度时,△AOD是等腰三角形.(直接写出答案)
【答案】(1)见解析;
(2)△AOD是Rt△.理由见解析;
(3)不能.理由:见解析;
(4)当α=110°或125°或140°时,△AOD是等腰三角形.
【解析】
(1)根据全等三角形的性质得到OC=DC,根据等边三角形的判定定理证明即可;
(2)根据全等三角形的性质得到∠ADC=∠BOC=∠α=150°,结合图形计算即可;
(3)用反证法,假设△AOD能否为等边三角形,根据题意证明∠AOC+∠AOB+∠BOC不等于360°,推出矛盾;
(4)分∠AOD=∠ADO、∠AOD=∠OAD、∠ADO=∠OAD三种情况,根据等腰三角形的判定定理计算即可.
(1)证明:∵△BOC≌△ADC,
∴OC=DC.
∵∠OCD=60°,
∴△OCD是等边三角形;
(2)△AOD是Rt△.
理由如下:
∵△OCD是等边三角形,
∴∠ODC=60°,
∵△BOC≌△ADC,∠α=150°,
∴∠ADC=∠BOC=∠α=150°,
∴∠ADO=∠ADC∠ODC=150°60°=90°,
∴△AOD是Rt△;
(3)不能.理由:
由△BOC≌△ADC,得∠ADC=∠BOC=∠α.
若△AOD为等边三角形,
则∠ADO=60°,
又∵∠ODC=60°,
∴∠ADC=∠α=120°.
又∵∠AOD=∠DOC=60°,
∴∠AOC=120°,
又∵∠AOB=110°,
∴∠AOC+∠AOB+∠BOC=120°+120°+110°=350°<360°.
∴△AOD不可能为等边三角形;
(4)∵△OCD是等边三角形,
∴∠COD=∠ODC=60°.
∵∠AOB=110°,∠ADC=∠BOC=α,
∴∠AOD=360°∠AOB∠BOC∠COD=360°110°α60°=190°α,
∠ADO=∠ADC∠ODC=α60°,
∴∠OAD=180°∠AOD∠ADO=180°(190°α)(α60°)=50°.
①当∠AOD=∠ADO时,190°α=α60°,∴α=125°.
②当∠AOD=∠OAD时,190°α=50°,∴α=140°.
③当∠ADO=∠OAD时,α60°=50°,∴α=110°.
综上所述:当α=110°或125°或140°时,△AOD是等腰三角形.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】为声援扬州“运河申遗”,某校举办了一次运河知识竞赛,满分10分,学生得分为整数,成绩达到6分以上(包括6分)为合格,达到9分以上(包含9分)为优秀.这次竞赛中甲乙两组学生成绩分布的条形统计图如图所示.

(1)补充完成下面的成绩统计分析表:
组别 | 平均分 | 中位数 | 方差 | 合格率 | 优秀率 |
甲组 | 6.7 | 3.41 | 90% | 20% | |
乙组 | 7.5 | 1.69 | 80% | 10% |
(2)小明同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上表可知,小明是 组的学生;(填“甲”或“乙”)
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你给出两条支持乙组同学观点的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市为加强学生的安全意识,组织了全市学生参加安全知识竞赛,为了解此次知识竞赛成绩的情况,随机抽取了部分参赛学生的成绩,整理并制作出如下的不完整的统计表和统计图,如图所示,请根据图表信息解答以下问题。
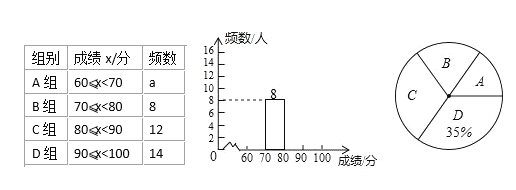
(1)一共抽取了___个参赛学生的成绩;表中a=___;
(2)补全频数分布直方图;
(3)计算扇形统计图中“B”对应的圆心角度数;
(4)某校共2000人,安全意识不强的学生(指成绩在70分以下)估计有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个机器人从数轴原点出发,沿数轴正方向,以每前进3步后退2步的程序运动。设该机器人每秒钟前进或后退1步,并且每步的距离是1个单位长,![]() 表示第
表示第![]() 秒时机器人在数轴上的位置所对应的数。给出下列结论:①
秒时机器人在数轴上的位置所对应的数。给出下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 。其中,正确的结论的序号是( )
。其中,正确的结论的序号是( )
A.①③B.②③C.①②③D.①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我县实施新课程改革后,学生的自主学习、合作交流能力有很大提高,胡老师为了了解班级学生自主学习、合作交流的具体情况,对某班部分学生进行了为期半个月的跟踪调查,并将调查结果分成四类,A:特别好;B:好;C:一般;D:较差;并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:
(1)本次调查中,胡老师一共调查了 名同学,其中女生共有 ___名;
(2)将上面的条形统计图补充完整;
(3)为了共同进步,胡老师想从被调查的A类和D类学生中分别选取一位同学进行“一帮一”互助学习,请用列表法或画树形图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率.
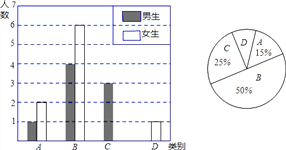
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,图案由边长相等的黑、白两色正方形按一定规律拼接而成,第n个图案中白色正方形的个数比黑色正方形的个数多_____.(用含有n的代数式表示)
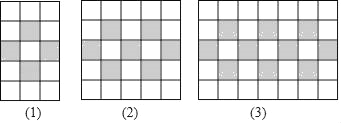
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市旅游景区有A,B,C,D,E等著名景点,该市旅游部门统计绘制出2018年春节期间旅游情况统计图(如图),根据图中信息解答下列问题:
(1)2018年春节期间,该市A,B,C,D,E这五个景点共接待游客 万人,扇形统计图中E景点所对应的圆心角的度数是 ,并补全条形统计图.
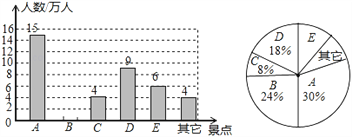
(2)甲,乙两个旅行团在A,B,D三个景点中随机选择一个,这两个旅行团选中同一景点的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A的坐标为(0,6),点B在x轴的正半轴上.若点P、Q在线段AB上,且PQ为某个一边与x轴平行的矩形的对角线,则称这个矩形为点P、Q的“涵矩形”。下图为点P、Q的“涵矩形”的示意图.
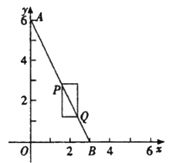
(1)点B的坐标为(3,0);
①若点P的横坐标为![]() ,点Q与点B重合,则点P、Q的“涵矩形”的周长为 .
,点Q与点B重合,则点P、Q的“涵矩形”的周长为 .
②若点P、Q的“涵矩形”的周长为6,点P的坐标为(1,4),则点E(2,1),F(1,2),G(4,0)中,能够成为点P、Q的“涵矩形”的顶点的是 .
(2)四边形PMQN是点P、Q的“涵矩形”,点M在△AOB的内部,且它是正方形;
①当正方形PMQN的周长为8,点P的横坐标为3时,求点Q的坐标.
②当正方形PMQN的对角线长度为/2时,连结OM.直接写出线段OM的取值范围 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com