
����Ŀ������Ϊ��ǿѧ���İ�ȫ��ʶ����֯��ȫ��ѧ���μӰ�ȫ֪ʶ������Ϊ�˽�˴�֪ʶ�����ɼ�������������ȡ�˲��ֲ���ѧ���ijɼ������������������µIJ�������ͳ�Ʊ���ͳ��ͼ����ͼ��ʾ�������ͼ����Ϣ����������⡣
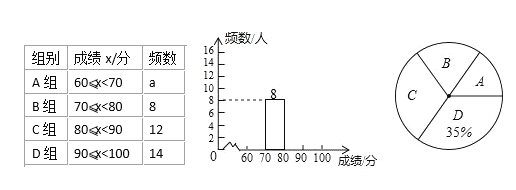
��1��һ����ȡ��___������ѧ���ijɼ�������a=___��
��2����ȫƵ���ֲ�ֱ��ͼ��
��3����������ͳ��ͼ����B����Ӧ��Բ�ĽǶ�����
��4��ijУ��2000�ˣ���ȫ��ʶ��ǿ��ѧ����ָ�ɼ���70�����£������ж����ˣ�
���𰸡���1��40��6����2������������3��72������4��300.
��������
��1�����������������֮��Ĺ�ϵ������⼴�ɣ�
��2������Ƶ���ֲ�����������ͼ���ɽ�����⣮
��3������Բ�Ľ�=360����ٷֱȼ��㼴�ɽ�����⣮
��4�����ݳɼ���70�����µİٷֱȳ������������ɣ�
(1)��ȡ��ѧ���ɼ���14��35%=40(��)��
��a=40(8+12+14)=6��
�ʴ�Ϊ��40��6��
(2)ֱ��ͼ��ͼ��ʾ��
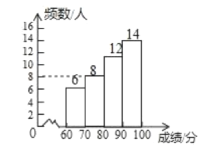
(3)����ͳ��ͼ����B����Բ�Ľ�=360���![]() =72��.
=72��.
(4) �ɼ���70�����£�![]() =300���ˣ�.
=300���ˣ�.


 �㽭��У��ʦ���ϵ�д�
�㽭��У��ʦ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��A��B�������ε��2010����2014�ꡰ�塢һ�������������仯����ֱ���ʵ�ߺ����߱�ʾ������ͼ����ʾ����������⣺

��1��B���ε���������������һ�꣬������������һ�ꣿ
��2����A��B�������ε��2010��2014������������ƽ�����ͷ������ƽ�����ͷ���ĽǶȣ���һ�仰�����������ε������������ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �ı߳�Ϊ
�ı߳�Ϊ![]() ����
����![]() ��
��![]() �ֱ��ڱ�
�ֱ��ڱ�![]() ��
��![]() �ϣ���
�ϣ���![]() ��
��![]() ���е㣬��
���е㣬��![]() ����
����![]() �ij�Ϊ_______��
�ij�Ϊ_______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
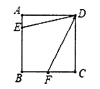
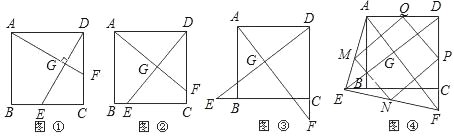
����Ŀ����ͼ1����������ABCD�У���E��F�ֱ�Ϊ��BC��CD���е㣬AF��DE�ཻ�ڵ�G����ɵý��ۣ���AF��DE����AF��DE������֤������
��1����ͼ��������E��F����������ABCD�ı�BC��CD���е㣬������CE��DF��������Ľ����������Ƿ���Ȼ����������ֱ�ӻش𡰳���������������
��2����ͼ��������E��F�ֱ���������ABCD�ı�CB���ӳ��ߺ�DC���ӳ����ϣ���CE��DF����ʱ����Ľ����������Ƿ���Ȼ����������������д��֤�����̣�������������˵�����ɣ�
��3����ͼ�����ڣ�2���Ļ����ϣ�����AE��EF������M��N��P��Q�ֱ�ΪAE��EF��FD��AD���е㣬�����ж��ı���MNPQ�ǡ����Ρ����Ρ������Ρ��������Ρ��е���һ�֣���д��֤�����̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��A��B��C��D�ĸ���վ��λ����ͼ��ʾ��A��B��վ֮��ľ���AB��a��b��B��C��վ֮��ľ���BC��2a��b��B��D��վ֮��ľ���BD��![]() a��2b��1����
a��2b��1����
��1��A��C��վ֮��ľ���AC��
��2����A��C��վ֮��ľ���AC��180km����C��D��վ֮��ľ���CD��
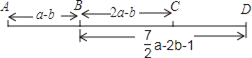
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
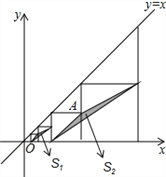
����Ŀ����ͼ����ƽ��ֱ������ϵ�У��߳����ȵ��������������У�ÿ�������ζ���һ���������ں���y=x��ͼ���ϣ��������ҵ�3���������е�һ������A������Ϊ��8��4������Ӱ�����β��ֵ���������������μ�ΪS1��S2��S3������Sn����Sn��ֵΪ__�����ú�n�Ĵ���ʽ��ʾ��nΪ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������龳
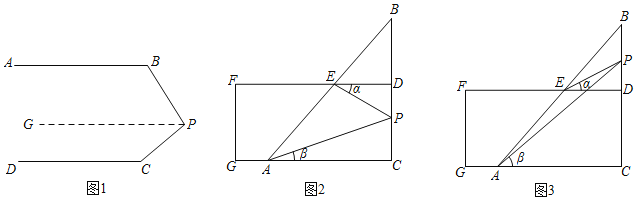
��1����ͼ1����֪AB��CD����PBA��125������PCD��155�������BPC�Ķ�����
����ͬѧ��˼·������P��PG��AB������PG��CD����ƽ���ߵ����������BPC����á�BPC���� ��
����Ǩ��
��2��ͼ2��ͼ3������һ�����ǰ��һ��ֱ��ƴ�ɵ�ͼ�Σ����ǰ����ֱ�DZ���ֱ�ߵ������غϣ���ACB��90����DF��CG��AB��FD�ཻ�ڵ�E����һ����P�ڱ�BC���˶�������PE��PA���ǡ�PED����������PAC��������
����ͼ2������P��C��D����֮���˶�ʱ����ֱ��д����APE�����������֮���������ϵ��
����ͼ3������P��B��D����֮���˶�ʱ����APE�����������֮���к�������ϵ�����жϲ�˵�����ɣ�
��չ����
��3������P��C��D����֮���˶�ʱ������PED����PAC�Ľ�ƽ����EN��AN�ཻ�ڵ�N����ֱ��д����ANE�����������֮���������ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O�ǵȱߡ�ABC��һ�㣬D�ǡ�ABC���һ�㣬��AOB��110�㣬��BOC��![]() ����BOC�ա�ADC����OCD��60�㣬����OD��
����BOC�ա�ADC����OCD��60�㣬����OD��
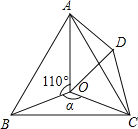
��1����֤����OCD�ǵȱ������Σ�
��2��������150��ʱ������֤����AOD��ֱ�������Σ�
��3����AOD�ܷ�Ϊ�ȱ������Σ�Ϊʲô��
��4��̽��������Ϊ���ٶ�ʱ����AOD�ǵ��������Σ���ֱ��д���𰸣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����ѧϰ������������ͼ��ʱ��������ʦҪ��ͬѧ�Ǹ��ݡ�̽��һ�κ���![]() ��ͼ�Ļ������裬��ֽ����̽������
��ͼ�Ļ������裬��ֽ����̽������![]() ��ͼ�����ںڰ���д��4��������꣺
��ͼ�����ںڰ���д��4��������꣺ ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
��
�� ��A��B��C��D�ĸ����У���ȡһ���㣬��������ֱ��![]() ����˫����
����˫����![]() �ϵĸ����Ƕ��٣�
�ϵĸ����Ƕ��٣�
�� С����A��B��C��D�ĸ�������ȡ�����������㣬�����㶼����˫����![]() �ϵĸ���.
�ϵĸ���.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com