
【题目】小明在学习反比例函数的图像时,他的老师要求同学们根据“探索一次函数![]() 的图像”的基本步骤,在纸上逐步探索函数
的图像”的基本步骤,在纸上逐步探索函数![]() 的图像,并且在黑板上写出4个点的坐标:
的图像,并且在黑板上写出4个点的坐标: ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
⑴ 在A、B、C、D四个点中,任取一个点,这个点既在直线![]() 又在双曲线
又在双曲线![]() 上的概率是多少?
上的概率是多少?
⑵ 小明从A、B、C、D四个点中任取两个点进行描点,求两点都落在双曲线![]() 上的概率.
上的概率.
【答案】(1)![]() ;⑵
;⑵![]()
【解析】试题分析:(1)把四个点 的坐标分别代入一次函数和反比例函数的解析式可知点B与点D既在直线y=x+1上,又在双曲线y=![]() 上,据此即可求得任取一个点,这个点既在直线y1=x+1又在双曲线y2=
上,据此即可求得任取一个点,这个点既在直线y1=x+1又在双曲线y2=![]() 上的概率.
上的概率.
(2)从A、B、C、D四个点中任意挑选两个点进行描点,有6种等可能的情况,分别是:AB,AC,AD,BC,BD,CD,其中,“两点都落在双曲线![]() 上”有AB、AD、BD 三种情况,从而求得两点都落在双曲线
上”有AB、AD、BD 三种情况,从而求得两点都落在双曲线![]() 的概率.
的概率.
试题解析:解:(1)把A、B、C、D分别代入y1=x+1和函数y2=![]() 可知:点B与点D既在直线y=x+1上,又在双曲线y=
可知:点B与点D既在直线y=x+1上,又在双曲线y=![]() 上,因此任取一个点,既在直线又在双曲线上的概率是
上,因此任取一个点,既在直线又在双曲线上的概率是![]() ;
;
(2)由(1)可得,“从A、B、C、D四个点中任意挑选两个点进行描点”
有6种等可能的情况,分别是:AB,AC,AD,BC,BD,CD,其中,“两点都落在双曲线![]() 上”有AB、AD、BD 三种情况.
上”有AB、AD、BD 三种情况.
故两点都落在双曲线![]() 的概率是:
的概率是: ![]() .
.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
【题目】我市为加强学生的安全意识,组织了全市学生参加安全知识竞赛,为了解此次知识竞赛成绩的情况,随机抽取了部分参赛学生的成绩,整理并制作出如下的不完整的统计表和统计图,如图所示,请根据图表信息解答以下问题。
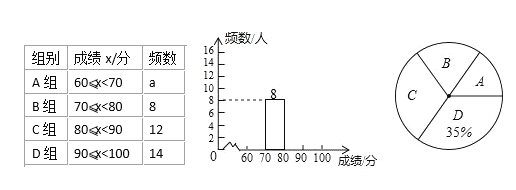
(1)一共抽取了___个参赛学生的成绩;表中a=___;
(2)补全频数分布直方图;
(3)计算扇形统计图中“B”对应的圆心角度数;
(4)某校共2000人,安全意识不强的学生(指成绩在70分以下)估计有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,图案由边长相等的黑、白两色正方形按一定规律拼接而成,第n个图案中白色正方形的个数比黑色正方形的个数多_____.(用含有n的代数式表示)
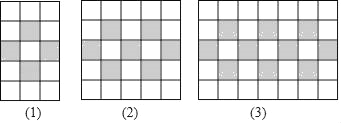
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市旅游景区有A,B,C,D,E等著名景点,该市旅游部门统计绘制出2018年春节期间旅游情况统计图(如图),根据图中信息解答下列问题:
(1)2018年春节期间,该市A,B,C,D,E这五个景点共接待游客 万人,扇形统计图中E景点所对应的圆心角的度数是 ,并补全条形统计图.
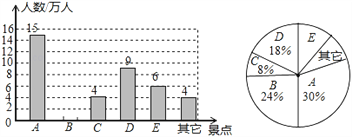
(2)甲,乙两个旅行团在A,B,D三个景点中随机选择一个,这两个旅行团选中同一景点的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国新版高铁“复兴号”率先在北京南站和上海虹桥站双向首发“复兴号”高铁从某车站出发,在行驶过程中速度![]() (千米/分钟)与时间
(千米/分钟)与时间![]() (分钟)的函数关系如图所示.
(分钟)的函数关系如图所示.

(1)当![]() 时,求
时,求![]() 关于
关于![]() 工的函数表达式,
工的函数表达式,
(2)求点![]() 的坐标.
的坐标.
(3)求高铁在![]() 时间段行驶的路程.
时间段行驶的路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2011年9月1日,长春首届航空开放日在长春大房身机场正式举行,空军八一飞行表演队的新换装歼-10飞机,进行了精彩的特技飞行表演,其中一架飞机起飞0.5千米后的高度变化如下表:
高度变化 | 上升4.2 | 下降3.5 | 上升1.4 | 下降1.2 |
记作 | +4.2 | -3.5 | +1.4 | -1.2 |
(1)此时这架飞机飞离地面的高度是多少千米?
(2)如果飞机做特技表演时,有4个规定动作,起飞后高度变化如下:上升3.6干米,下降2.8千米,再上升1.5千米,最后下降0.9千米.若飞机平均上升1干米需消耗6升燃油,平均下降1千米需消耗4升燃油,那么这架飞机在这4个特技表演过程中,一共消耗了多少升燃油?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新春佳节,电子鞭炮因其安全、无污染开始走俏.某商店经销一种电子鞭炮,已知这种电子鞭炮的成本价为每盒80元,市场调查发现,该种电子鞭炮每天的销售量y(盒)与销售单价x(元)有如下关系:y=﹣2x+320(80≤x≤160).设这种电子鞭炮每天的销售利润为w元.
(1)求w与x之间的函数关系式;
(2)该种电子鞭炮销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3)该商店销售这种电子鞭炮要想每天获得2400元的销售利润,又想买得快.那么销售单价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A的坐标为(0,6),点B在x轴的正半轴上.若点P、Q在线段AB上,且PQ为某个一边与x轴平行的矩形的对角线,则称这个矩形为点P、Q的“涵矩形”。下图为点P、Q的“涵矩形”的示意图.
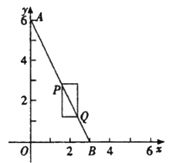
(1)点B的坐标为(3,0);
①若点P的横坐标为![]() ,点Q与点B重合,则点P、Q的“涵矩形”的周长为 .
,点Q与点B重合,则点P、Q的“涵矩形”的周长为 .
②若点P、Q的“涵矩形”的周长为6,点P的坐标为(1,4),则点E(2,1),F(1,2),G(4,0)中,能够成为点P、Q的“涵矩形”的顶点的是 .
(2)四边形PMQN是点P、Q的“涵矩形”,点M在△AOB的内部,且它是正方形;
①当正方形PMQN的周长为8,点P的横坐标为3时,求点Q的坐标.
②当正方形PMQN的对角线长度为/2时,连结OM.直接写出线段OM的取值范围 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一次函数y1=k1x+2的图象与反比例函数y2=![]() 的图象交于点A(4,m)和B(-8,-2),与y轴交于点C.
的图象交于点A(4,m)和B(-8,-2),与y轴交于点C.

(1)k1=__________,k2=__________;
(2)根据函数图象可知,当y1>y2时,x的取值范围是____________;
(3)过点A作AD⊥x轴于点D,点P是反比例函数在第一象限的图象上一点.设直线OP与线段AD交于点E,当S四边形ODACS△ODE=31时,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com