
【题目】如图,ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=![]() BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE=
BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE=![]() BC,成立的个数有( )
BC,成立的个数有( )
A.1个
B.2个
C.3个
D.4个
【答案】C
【解析】∵四边形ABCD是平行四边形,∴∠ABC=∠ADC=60°,∠BAD=120°,∵AE平分∠BAD,∴∠BAE=∠EAD=60°∴△ABE是等边三角形,
∴AE=AB=BE,∵AB=![]() BC,∴AE=
BC,∴AE=![]() BC,∴∠BAC=90°,∴∠CAD=30°,故①正确;∵AC⊥AB,∴SABCD=ABAC,故②正确,
BC,∴∠BAC=90°,∴∠CAD=30°,故①正确;∵AC⊥AB,∴SABCD=ABAC,故②正确,
∵AB=![]() BC,OB=
BC,OB=![]() BD,∵BD>BC,∴AB≠OB,故③错误;∵CE=BE,CO=OA,∴OE=
BD,∵BD>BC,∴AB≠OB,故③错误;∵CE=BE,CO=OA,∴OE=![]() AB,∴OE=
AB,∴OE=![]() BC,故④正确.故选:C.
BC,故④正确.故选:C.
由四边形ABCD是平行四边形,得到∠ABC=∠ADC=60°,∠BAD=120°,根据AE平分∠BAD,得到∠BAE=∠EAD=60°推出△ABE是等边三角形,由于AB=![]() BC,得到AE=
BC,得到AE=![]() BC,得到△ABC是直角三角形,于是得到∠CAD=30°,故①正确;由于AC⊥AB,得到SABCD=ABAC,故②正确,根据AB=
BC,得到△ABC是直角三角形,于是得到∠CAD=30°,故①正确;由于AC⊥AB,得到SABCD=ABAC,故②正确,根据AB=![]() BC,OB=
BC,OB=![]() BD,且BD>BC,得到AB≠OB,故③错误;根据三角形的中位线定理得到OE=
BD,且BD>BC,得到AB≠OB,故③错误;根据三角形的中位线定理得到OE=![]() AB,于是得到OE=
AB,于是得到OE=![]() BC,故④正确.
BC,故④正确.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为坐标原点,抛物线y=﹣x2+bx+3与x轴交于点A(1,0)和点B,与y轴交于点C.
(1)求抛物线的解析式.
(2)直线y=kx+3k经过点B,与y轴的负半轴交于点D,点P为第二象限内抛物线上一点,连接PD,射线PD绕点P顺时针旋转与线段BD交于点E,且∠EPD=2∠PDC,∠EPD的平分线交线段BD于点H,∠BEP+∠BDP=90°
①若四边形PHDC是平行四边形,求点P的坐标;
②过点E作EF⊥PD,交PD于点G,交y轴于点F,已知PF=3 ![]() ,求直线PF的解析式.
,求直线PF的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学开展“阳光体育一小时”活动,根据学校实际情况,如图决定开设“A:踢毽子,B:篮球,C:跳绳,D:乒乓球”四项运动项目(每位同学必须选择一项),为了解学生最喜欢哪一项运动项目,随机抽取了一部分学生进行调查,丙将调查结果绘制成如图的统计图,则参加调查的学生中最喜欢跳绳运动项目的学生数为( )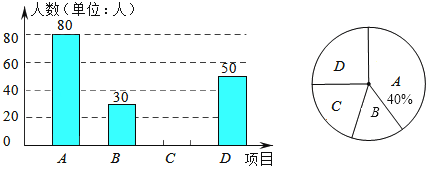
A.240
B.120
C.80
D.40
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂现有甲种原料360千克,乙种原料290千克,计划用这两种原料全部生产A、B两种产品共50件,生产A、B两种产品与所需原料情况如下表所示:
原料型号 | 甲种原料(千克) | 乙种原料(千克) |
A产品(每件) | 9 | 3 |
B产品(每件) | 4 | 10 |
(1)该工厂生产A、B两种产品有哪几种方案?
(2)若生成一件A产品可获利80元,生产一件B产品可获利120元,怎样安排生产可获得最大利润?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有甲、乙两个容器,分别装有进水管和出水管,两容器的进出水速度不变,先打开乙容器的进水管,2分钟时再打开甲容器的进水管,又过2分钟关闭甲容器的进水管,再过4分钟同时打开甲容器的进、出水管.直到12分钟时,同时关闭两容器的进出水管.打开和关闭水管的时间忽略不计.容器中的水量y(升)与乙容器注水时间x(分)之间的关系如图所示.
(1)求甲容器的进、出水速度.
(2)甲容器进、出水管都关闭后,是否存在两容器的水量相等?若存在,求出此时的时间.
(3)若使两容器第12分钟时水量相等,则乙容器6分钟后进水速度应变为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有三张反面朝上的扑克牌:红桃2、红桃3、黑桃x(1≤x≤13且x为奇数或偶数).把牌洗匀后第一次抽取一张,记好花色和数字后将牌放回,重新洗匀第二次再抽取一张.
(1)求两次抽得相同花色的概率;
(2)当甲选择x为奇数,乙选择x为偶数时,他们两次抽得的数字和是奇数的可能性大小一样吗?请说明理由.(提示:三张扑克牌可以分别简记为红2、红3、黑x)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=x2﹣4x+3与x轴交于A、B两点(点A在点B的左侧),点C是此抛物线的顶点.
(1)求点A、B、C的坐标;
(2)点C在反比例函数![]() (k≠0)的图象上,求反比例函数的解析式.
(k≠0)的图象上,求反比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有四张正面分别标有数字﹣1,0,1,2的不透明卡片,它们除数字外其余全部相同,现将它们背面朝上洗均匀.
(1)随机抽取一张卡片,求抽到数字“﹣1”的概率;
(2)随机抽取一张卡片,然后不放回,再随机抽取一张卡片,请用列表或画树状图的方法求出第一次抽到数字“2”且第二次抽到数字“0”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com