
【题目】如图,在平面直角坐标系中,O为坐标原点,抛物线y=﹣x2+bx+3与x轴交于点A(1,0)和点B,与y轴交于点C.
(1)求抛物线的解析式.
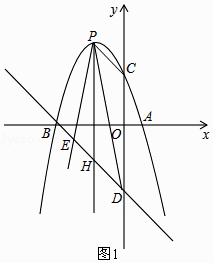
(2)直线y=kx+3k经过点B,与y轴的负半轴交于点D,点P为第二象限内抛物线上一点,连接PD,射线PD绕点P顺时针旋转与线段BD交于点E,且∠EPD=2∠PDC,∠EPD的平分线交线段BD于点H,∠BEP+∠BDP=90°
①若四边形PHDC是平行四边形,求点P的坐标;
②过点E作EF⊥PD,交PD于点G,交y轴于点F,已知PF=3 ![]() ,求直线PF的解析式.
,求直线PF的解析式.
【答案】
(1)
解:把A(1,0)代入y=﹣x2+bx+3中,
﹣1+b+3=0,解得:b=﹣2,
∴抛物线的解析式为:y=﹣x2﹣2x+3;
(2)
解:如图1,当y=0时,﹣x2﹣2x+3=0,
x2+2x﹣3=0,
(x+3)(x﹣1)=0,
x1=﹣3,x2=1,
∴B(﹣3,0),
∵四边形PHDC是平行四边形,
∴PH∥DC,
∴∠EHP=∠EDC,∠HPD=∠PDC,
设∠PDC=x,∠BDP=y,则∠EPH=∠HPD=x,∠EHP=∠EDC=x+y,
∴∠BEP=∠BHP+∠EPH=x+y+x=2x+y,
∵∠BEP+∠BDP=90°,
∴2x+y+y=90°,
x+y=45°,
即∠BHP=45°,
∴∠BDC=45°,
∴△BOD是等腰直角三角形,
∴OB=OD=3=﹣3k,
k=﹣1,
∴直线BD的解析式为:y=﹣x﹣3,
∵PH⊥x轴,
设P(x,﹣x2﹣2x+3),H(x,﹣x﹣3),
∴PH=CD=6,
∴﹣x2﹣2x+3+x+3=6,
解得:x1=0(舍),x2=﹣1,
∴P(﹣1,4);
②如图2,过D作DQ⊥y轴交PE的延长线于Q,直线PH交DQ于M,PN⊥y轴于N,
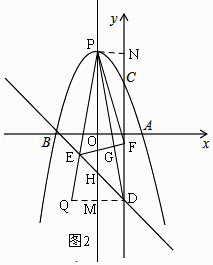
∵∠PDC= ![]() ∠EPD=∠DPH,
∠EPD=∠DPH,
∴PM∥DN,
∵DQ⊥DN,
而PM平分∠QPD,
∴MQ=MD,
易得四边形PNDM为矩形,
∴MD=PN,
∴DQ=2PN,
∵EF⊥PD,
∴∠BDP+∠DEG=90°,
而∠BDP+∠BEP=90°,
∴∠DEG=∠BEP=∠QED,
∵∠BDF=45°,
∴∠QDE=45°,
在△DEQ和△DEF中,
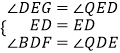 ,
,
∴△DEQ≌△DEF(ASA),
∴DQ=DF,
∴DF=2MD=2PN,
设P(x,﹣x2﹣2x+3),则PN=DM=﹣x,DF=﹣2x,FN=﹣x2﹣2x+3+3+2x=﹣x2+6,
在Rt△PFN中,由勾股定理得:PF2=PN2+FN2,
∴ ![]() =(﹣x)2+(﹣x2+6)2,
=(﹣x)2+(﹣x2+6)2,
解得:x1= ![]() ,x2=±3,
,x2=±3,
∵点P为第二象限内抛物线上一点,
∴x=﹣ ![]() ,
,
∴DF=2 ![]() ,
,
∴P(﹣ ![]() ,2
,2 ![]() ﹣3),F(0,2
﹣3),F(0,2 ![]() ﹣3),
﹣3),
设PF解析式为:y=kx+b,
把P(﹣ ![]() ,2
,2 ![]() ﹣3),F(0,2
﹣3),F(0,2 ![]() ﹣3)代入得:
﹣3)代入得:
![]() ,
,
∴ ![]() ,
,
∴直线PF的解析式为:y=﹣2 ![]() x+2
x+2 ![]() ﹣3.
﹣3.
【解析】(1)把点A的坐标代入抛物线的解析式中可得结论;(2)①如图1,推出∠BHP=45°,求出直线BD解析式:y=﹣x﹣3,求出P点坐标等于(﹣1,4);②如图2,作辅助线,构建矩形和等腰三角形,判断四边形PNDM为矩形得到MD=PN,则DQ=2PN,然后证明△DEQ≌△DEF得到DQ=DF,所以DF=2MD=2PN;再在Rt△PFN中利用勾股定理列方程得出P和F的坐标,根据待定系数法求直线PF的解析式.
【考点精析】认真审题,首先需要了解二次函数的性质(增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小),还要掌握等腰三角形的性质(等腰三角形的两个底角相等(简称:等边对等角))的相关知识才是答题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】在矩形ABCD中, ![]() =a,点G,H分别在边AB,DC上,且HA=HG,点E为AB边上的一个动点,连接HE,把△AHE沿直线HE翻折得到△FHE.
=a,点G,H分别在边AB,DC上,且HA=HG,点E为AB边上的一个动点,连接HE,把△AHE沿直线HE翻折得到△FHE.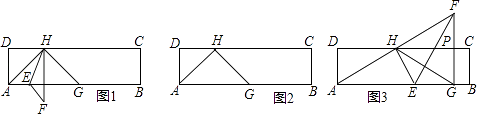
(1)如图1,当DH=DA时,填空:∠HGA=度;
(2)如图1,当DH=DA时,若EF∥HG,求∠AHE的度数,并求此时的最小值;
(3)如图3,∠AEH=60°,EG=2BG,连接FG,交边DC于点P,且FG⊥AB,G为垂足,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】经市场调查,某种商品在第x天的售价与销量的相关信息如下表;已知该商品的进价为每件30元,设销售该商品每天的利润为y元. 
(1)求出y与x的函数关系式
(2)问销售该商品第几天时,当天销售利润最大?最大利润是多少?
(3)该商品销售过程中,共有多少天日销售利润不低于4800元?直接写出答案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙、丙3人聚会,每人带了一件礼物,将这3件礼物分别放在3个完全相同的盒子里,每人随机抽取一个礼盒(装有礼物的盒子)
(1)下列事件是必然事件的是 A 乙没有抽到自己带来的礼物B 乙恰好抽到自己带来的礼物C 乙抽到一件礼物D 只有乙抽到自己带来的礼物
(2)甲、乙、丙3人抽到的都不是自己带来的礼物(记为事件A),请列出事件A的所有可能的结果,并求事件A的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某数学兴趣小组在活动课上测量学校旗杆高度.已知小明的眼睛与地面的距离AB=1.7m,看旗杆顶部M的仰角为45°;小红的眼睛与地面的距离CD=1.5m,看旗杆顶部M的仰角为30°.两人相距28米且位于旗杆两侧(点B、N、D在同一条直线上).请求出旗杆MN的高度.(参考数据: ![]() ≈1.4,
≈1.4, ![]() ≈1.7,结果保留整数)
≈1.7,结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的对角线AC、BD交于点O,AE平分∠BAD交BC于点E,且∠ADC=60°,AB=![]() BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE=
BC,连接OE.下列结论:①∠CAD=30°;②SABCD=ABAC;③OB=AB;④OE=![]() BC,成立的个数有( )
BC,成立的个数有( )
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com