练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，已知某广场菱形花坛ABCD的周长是24米，∠BAD=60°，则花坛对角线AC的长等于（ ）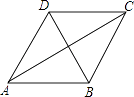
    A.6 米
    B.6米
    C.3 米
    D.3米

    【答案】A
    【解析】解：∵四边形ABCD为菱形， ∴AC⊥BD，OA=OC，OB=OD，AB=BC=CD=AD=24÷4=6（米），
    ∵∠BAD=60°，
    ∴△ABD为等边三角形，
    ∴BD=AB=6（米），OD=OB=3（米），
    在Rt△AOB中，根据勾股定理得：OA= =3 （米），
    则AC=2OA=6 米，
    故选A．

    【考点精析】利用菱形的性质对题目进行判断即可得到答案，需要熟知菱形的四条边都相等；菱形的对角线互相垂直，并且每一条对角线平分一组对角；菱形被两条对角线分成四个全等的直角三角形；菱形的面积等于两条对角线长的积的一半．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，在破残的圆形残片上，弦AB的垂直平分线交弧AB于点C，交弦AB于点D，已知AB=8 cm，CD=2 cm．求破残的圆形残片的半径．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知方程 ，且关于x的不等式组 只有4个整数解，那么b的取值范围是（ ）
    A.﹣1＜b≤3
    B.2＜b≤3
    C.8≤b＜9
    D.3≤b＜4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在信息快速发展的社会，“信息消费”已成为人们生活的重要组成部分．某高校组织课外小组在郑州市的一个社区随机抽取部分家庭，调查每月用于信息消费的金额，根据数据整理成如图所示的不完整统计表和统计图．已知A，B两组户数频数直方图的高度比为1：5．
    月信息消费额分组统计表

    组别

    消费额（元）

    A

    10≤x＜100

    B

    100≤x＜200

    C

    20≤x＜300

    D

    300≤x＜400

    E

    x≥400

    请结合图表中相关数据解答下列问题：

    （1）这次接受调查的有户；
    （2）在扇形统计图中，“E”所对应的圆心角的度数是；
    （3）请你补全频数直方图；
    （4）若该社区有2000户住户，请估计月信息消费额不少于200元的户数是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，这是一把可调节座椅的侧面示意图，已知头枕上的点A到调节器点O处的距离为80cm，AO与地面垂直，现调整靠背，把OA绕点O旋转35°到OA′处，求调整后点A′比调整前点A的高度降低了多少厘米（结果取整数）？ （参考数据：sin35°≈0.57，cos35°≈0.82，tan35°≈0.70）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，将矩形ABCD沿DE折叠，使顶点A落在DC上的点A′处，然后将矩形展平，沿EF折叠，使顶点A落在折痕DE上的点G处．再将矩形ABCD沿CE折叠，此时顶点B恰好落在DE上的点H处．如图2．
    （1）求证：EG=CH；
    （2）已知AF= ，求AD和AB的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，在△ABC中，CD为AB边上的中线，点E、F分别在线段CD、AD上，且 ．点G是EF的中点，射线DG交AC于点H．

    （1）求证：△DFE∽△DAC；
    （2）请你判断点H是否为AC的中点？并说明理由；
    （3）若将△ADH绕点D顺时针旋转至△A′DH′，使射线DH′与射线CB相交于点M（不与B，C重合．图2是旋转后的一种情形），请探究∠BMD与∠BDA′之间所满足的数量关系，并加以证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我市民营经济持续发展，2015年城镇民营企业就业人数突破20万．为了解城镇民营企业员工每月的收入状况，统计局对全市城镇民营企业员工2015年月平均收入随机抽样调查，将抽样的数据按“2000元以内”、“2000元～4000元”、“4000元～6000元”和“6000元以上”分为四组，进行整理，分别用A，B，C，D表示，得到下列两幅不完整的统计图．

    由图中所给出的信息解答下列问题：
    （1）本次抽样调查的员工有人，在扇形统计图中x的值为 ， 表示“月平均收入在2000元以内”的部分所对应扇形的圆心角的度数是；
    （2）将不完整的条形图补充完整，并估计我市2015年城镇民营企业20万员工中，每月的收入在“2000元～4000元”的约多少人？
    （3）统计局根据抽样数据计算得到，2016年我市城镇民营企业员工月平均收入为4872元，请你结合上述统计的数据，谈一谈用平均数反映月收入情况是否合理？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，O为坐标原点，抛物线y=﹣x2+bx+3与x轴交于点A（1，0）和点B，与y轴交于点C．

    （1）求抛物线的解析式．
    （2）直线y=kx+3k经过点B，与y轴的负半轴交于点D，点P为第二象限内抛物线上一点，连接PD，射线PD绕点P顺时针旋转与线段BD交于点E，且∠EPD=2∠PDC，∠EPD的平分线交线段BD于点H，∠BEP+∠BDP=90°
    ①若四边形PHDC是平行四边形，求点P的坐标；
    ②过点E作EF⊥PD，交PD于点G，交y轴于点F，已知PF=3 ，求直线PF的解析式．

    查看答案和解析>>

    同步练习册答案