
����Ŀ������Ϣ���ٷ�չ����ᣬ����Ϣ���ѡ��ѳ�Ϊ�����������Ҫ��ɲ��֣�ij��У��֯����С����֣���е�һ�����������ȡ���ּ�ͥ������ÿ��������Ϣ���ѵĽ�����������������ͼ��ʾ�IJ�����ͳ�Ʊ���ͳ��ͼ����֪A��B���黧��Ƶ��ֱ��ͼ�ĸ߶ȱ�Ϊ1��5��
����Ϣ���Ѷ����ͳ�Ʊ�
��� | ���ѶԪ�� |
A | 10��x��100 |
B | 100��x��200 |
C | 20��x��300 |
D | 300��x��400 |
E | x��400 |
����ͼ����������ݽ���������⣺
��1����ν��ܵ����������
��2��������ͳ��ͼ�У���E������Ӧ��Բ�ĽǵĶ�������
��3�����㲹ȫƵ��ֱ��ͼ��
��4������������2000��ס�������������Ϣ���Ѷ����200Ԫ�Ļ����Ƕ��٣�
���𰸡�
��1��50
��2��28.8��
��3���⣺C���Ƶ���ǣ�50��40%=20����ͼ��
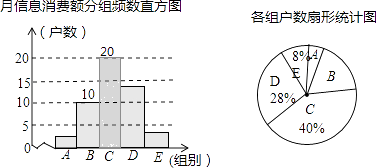
��4���⣺2000����28%+8%+40%��=1520��������
�𣺹�������Ϣ���Ѷ����200Ԫ��Լ��1520��
���������⣺��1��A���Ƶ���ǣ�10�� ![]() =2��
=2��
����ν��ܵ�����У�2+10���£�1��8%��28%��40%��=50��������
�ʴ�Ϊ��50����2����E������Ӧ��Բ�ĽǵĶ�����360���8%=28.8�㣬
�ʴ�Ϊ��28.8�㣻
��1������A��B���黧��ֱ��ͼ�ĸ߶ȱ�Ϊ1��5���������Ƶ���ı���1��5���ݴ˼������A���Ƶ��������A��B�����Ƶ���ĺͳ���������ռ�İٷֱȼ��������������2���á�E����ٷֱȳ���360��ɵã���3�������������ٷֱȼ������C���Ƶ�����Ӷ���ȫͳ��ͼ����4����������2000����C��D��E�İٷֱȼ��ɣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����һ���ʵ���ֱ�������εĻ�ľ�У����ڻ�ľ����ֻʣ����ͼ1��ʾ�ľŸ��ո�ͼ2�ǿɹ�ѡ���A��B��C��D�Ŀ��ľ�� 
��1��С��ѡ��ѻ�ľA��B����ͼ3��Ҫ���ľA��B�ľŸ�СԲǡ���ֱܷ���ͼ3�еľŸ�СԲ�غϣ�����ͼ3�л��������뷽ʽ��ʾ��ͼ����ܰ���ѣ���ľA��B������СԲ��С�߶λ���Ҫ����Ŷ������
��2���ִ�A��B��C��D�Ŀ��ľ����ѡ���飬�����б�������״ͼ����ǡ����ȫ�����ص�����ĸ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪���κ���y=x2+bx+c��ͼ����x�ύ��A��B���㣬��y�ύ�ڵ�P������ΪC��1����2����
��1����˺����Ĺ�ϵʽ��
��2������C����x��ĶԳƵ�D��˳������A��C��B��D�������������ϴ��ڵ�E��ʹֱ��PE���ı���ACBD�ֳ������ȵ������ı��Σ����E�����ꣻ
��3���ڣ�2���������£����������Ƿ����һ��F��ʹ�á�PEF����PΪֱ�Ƕ����ֱ�������Σ������ڣ������F�����꼰��PEF��������������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A��ֱ��l��һ�㣬��l��ȡ����B��C���ֱ���A��CΪԲ�ģ�BC��AB�ij�Ϊ�뾶�������������ڵ�D���ֱ�����AB��AD��CD������ABC+��ADC=120�㣬���A�Ķ����ǣ� �� 
A.100��
B.110��
C.120��
D.125��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=��x2+bx+c��x���ཻ��A��B���㣬��y���ཻ�ڵ�C���ҵ�B���C������ֱ�ΪB��3��0����C��0��3������M�������ߵĶ��㣮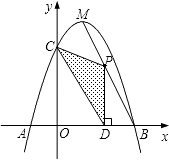
��1������κ����Ĺ�ϵʽ��
��2����PΪ�߶�MB��һ�����㣬����P��PD��x���ڵ�D����OD=m����PCD�����ΪS�����ж�S�����ֵ����Сֵ����˵�����ɣ�
��3����MB���Ƿ���ڵ�P��ʹ��PCDΪֱ�������Σ�������ڣ���ֱ��д����P�����ꣻ��������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪ij�㳡���λ�̳ABCD���ܳ���24�ף���BAD=60�㣬��̳�Խ���AC�ij����ڣ� �� 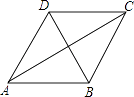
A.6 ![]() ��
��
B.6��
C.3 ![]() ��
��
D.3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У�AD��BC��DE��BC������Ϊ��E������AC��DE�ڵ�F����GΪAF���е㣬��ACD=2��ACB����DG=3��EC=1����DE�ij�Ϊ�� ��
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����г����飬ij����Ʒ�ڵ�x����ۼ��������������Ϣ���±�����֪����Ʒ�Ľ���Ϊÿ��30Ԫ�������۸���Ʒÿ�������ΪyԪ�� 
��1�����y��x�ĺ�����ϵʽ
��2�������۸���Ʒ�ڼ���ʱ�������������������������Ƕ��٣�
��3������Ʒ���۹����У����ж�����������������4800Ԫ��ֱ��д���𰸣�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com