
【题目】如图,在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF;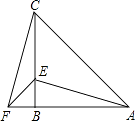
(1)求证:Rt△ABE≌Rt△CBF;
(2)求证:AB=CE+BF;
(3)若∠CAE=30°,求∠ACF度数.
【答案】
(1)证明:∵∠ABC=90°,
∴∠ABE=∠CBF=90°,
在Rt△ABE和Rt△CBF中,
![]() ,
,
∴Rt△ABE≌Rt△CBF(HL)
(2)证明:∵Rt△ABE≌Rt△CBF,
∴AB=BC,BE=BF,
∵BC=BE+CE,
∴AB=CE+BF
(3)∵AB=CB,∠ABC=90°,∠CAE=30°,∠CAB=∠CAE+∠EAB,
∴∠BCA=∠BAC=45°,
∴∠EAB=15°,
∵Rt△ABE≌Rt△CBF,
∴∠EAB=∠FCB,
∴∠FCB=15°,
∴∠ACF=∠FCB+∠BCA=15°+45°=60°,
即∠ACF=60°
【解析】(1)易由由所给条件已有“HL”得到Rt△ABE≌Rt△CBF。
(2)由(1)得Rt△ABE≌Rt△CBF,可由等量代换得到AB=CE+BF;
(3)由等腰直角三角形性质易得∠BCA=∠BAC=45°题干给了∠CAE=30°,所以易得∠EAB=15°,由(1)中相似可知∠FCB=15°即∠ACF=60°


科目:初中数学 来源: 题型:
【题目】某种计算机完成一次基本运算的时间约为0.000000005s,把0.000000005s用科学记数法可以表示为( )
A.0.5×10﹣8s
B.5×10﹣9s
C.5×10﹣8s
D.0.5×10﹣9s
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D是BA延长线上的一点,点E是AC的中点.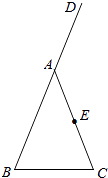
(1)实践与操作:利用尺规按下列要求作图,并在图中标明相应字母(保留作图痕迹,不写作法);
①作∠DAC的平分线AM;
②连接BE并延长交AM于点F;
(2)猜想与证明:试猜想AF与BC有怎样的位置关系和数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某通讯公司推出甲、乙两种通讯收费方式供用户选择,其中一种有月租费,另一种无月租费,且两种收费方式的通讯时间x(分钟)与收费y(元)之间的函数关系如图所示.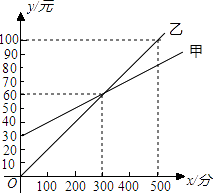
(1)有月租费的收费方式是(填甲或乙),月租费是元;
(2)求出甲、乙两种收费方式中y与自变量x之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E、F分别是□ABCD的边BC、AD上的点,且BE=DF.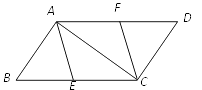
(1)求证:四边形AECF是平行四边形;
(2)若BC=10,∠BAC=90°,且四边形AECF是菱形,求BE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com