
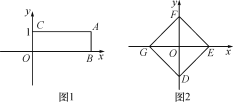
【题目】(11分)如图1,点A(a,b)在平面直角坐标系xOy中,点A到坐标轴的垂线段AB,AC与坐标轴围成矩形OBAC,当这个矩形的一组邻边长的和与积相等时,点A称作“垂点”,矩形称作“垂点矩形”.
(1)在点P(1,2),Q(2,-2),N(![]() ,-1)中,是“垂点”的点为 ;
,-1)中,是“垂点”的点为 ;
(2)点M(-4,m)是第三象限的“垂点”,直接写出m的值 ;
(3)如果“垂点矩形”的面积是![]() ,且“垂点”位于第二象限,写出满足条件的“垂点”的坐标 ;
,且“垂点”位于第二象限,写出满足条件的“垂点”的坐标 ;
(4)如图2,平面直角坐标系的原点O是正方形DEFG的对角线的交点,当正方形DEFG的边上存在“垂点”时,GE的最小值为8.
【答案】(1)Q;(2)-![]() ;(3)(-4,
;(3)(-4,![]() ),(-
),(-![]() ,4);(4)8
,4);(4)8
【解析】
(1)根据“垂点”的意义直接判断即可得出结论;
(2)根据“垂点”的意义建立方程即可得出结论;
(3)根据“垂点”的意义和矩形的面积建立方程即可得出结论;
(4)先确定出直线EF的解析式,利用“垂点”的意义建立方程,利用非负性即可确定出m的范围,即可得出结论.
(1)∵P(1,2),∴1+2=3,1×2=2,
∵2≠3,∴点P不是“垂点”,
∵Q(2,﹣2),∴2+2=4,2×2=4,∴Q是“垂点”.
∵N(![]() ,﹣1),∴
,﹣1),∴![]() +1=
+1=![]() ×1=
×1=![]() ,
,
∵![]() ,∴点N不是“垂点”,
,∴点N不是“垂点”,
故答案为:Q;
(2)∵点 M(﹣4,m)是第三象限的“垂点”,∴4+(﹣m)=4×(﹣m),∴m=﹣![]() ,
,
故答案为:﹣![]() ;
;
(3)设“垂点”的坐标为(a,b),∴﹣a+b=﹣ab,
∵“垂点矩形”的面积为![]() ,∴﹣ab=
,∴﹣ab=![]() .
.
即:﹣a+b=﹣ab=![]() ,
,
解得:a=﹣4,b=![]() 或a=﹣
或a=﹣![]() ,b=4,∴“垂点”的坐标为(﹣4,
,b=4,∴“垂点”的坐标为(﹣4,![]() )或(﹣
)或(﹣![]() ,4),
,4),
故答案为:(﹣4,![]() )或(﹣
)或(﹣![]() ,4),.
,4),.
(4)设点E(m,0)(m>0),
∵四边形EFGH是正方形,∴F(0,m),y=﹣x+m.设边EF上的“垂点”的坐标为(a,﹣a+m),∴a+(﹣a+m)=a(﹣a+m)
∴a2﹣am=﹣m,∴(a﹣![]() )2=
)2=![]() ≥0,∴m2﹣4m=m(m﹣4)≥0,
≥0,∴m2﹣4m=m(m﹣4)≥0,
∵m>0,∴m﹣4≥0,∴m≥4,∴m的最小值为4,∴EG的最小值为2m=8,
故答案为:8.


科目:初中数学 来源: 题型:
【题目】如图,∠B、∠D的两边分别平行。

(1)在图①中,∠B与∠D的数量关系为相等相等。
(2)在图②中,∠B与∠D的数量关系为互补互补。
(3)用一句话归纳的结论为如果一个角的两边分别平行于另一个角的两边,那么这两个角相等或互补如果一个角的两边分别平行于另一个角的两边,那么这两个角相等或互补。
试分别说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是边长为1的正方形,点E在AD边上运动,且不与点A和点D重合,连结CE,过点C作CF⊥CE交AB的延长线于点F,EF交BC于点G.
(1)求证:△CDE≌△CBF;
(2)当DE=![]() 时,求CG的长;
时,求CG的长;
(3)连结AG,在点E运动过程中,四边形CEAG能否为平行四边形?若能,求出此时DE的长;若不能,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=2,∠DAB=60°,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD,AN.

(1)求证:四边形AMDN是平行四边形;
(2)填空:①当AM的值为 时,四边形AMDN是矩形;②当AM的值为 时,四边形AMDN是菱形。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市政府大力扶持大学生创业.李明在政府的扶持下投资销售一种进价为每件20元的护眼台灯.销售过程中发现,每月销售量y(件)与销售单价x(元)之间的关系可近似的看作一次函数: ![]() .
.
(1)设李明每月获得利润为w(元),当销售单价定为多少元时,每月可获得最大利润?
(2)如果李明想要每月获得2000元的利润,那么销售单价应定为多少元?
(3)根据物价部门规定,这种护眼台灯的销售单价不得高于32元,如果李明想要每月获得的利润不低于2000元,那么他每月的成本最少需要多少元?(成本=进价×销售量)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,BC为⊙O的切线,D为⊙O上的一点,CD=CB,延长CD交BA的延长线于点E.
(1)求证:CD为⊙O的切线;
(2)若BD的弦心距OF=1,∠ABD=30°,求图中阴影部分的面积.(结果保留π)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,动点P按图中箭头所示方向从原点出发,第1次运动到P1(1,1),第2次接着运动到点P2(2,0),第3次接着运动到点P3(3,-2),…,按这的运动规律,点P2019的坐标是_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com