
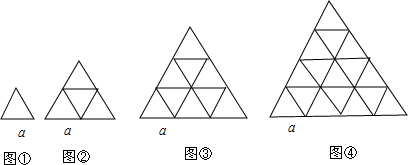
���� ��1��ͼ�������εı߳�Ϊa����Ҫ�߳�Ϊa��С������1����ͼ�������εı߳�Ϊ2a����Ҫ�߳�Ϊa��С������1+3=4����ͼ�������εı߳�Ϊ3a����Ҫ�߳�Ϊa��С������1+3+5=9�������ɴ˵ó�ͼn�����εı߳�Ϊna����Ҫ�߳�Ϊa��С������1+3+5+��+2n-1=n2������һ���ó�ƴ�ɵ������εı߳�Ϊ5a����Ҫ�߳�Ϊa��С������1+3+5+7+9=25����
��2��ͼ����Ҫ�߳�Ϊa��С������1+3+5+7=16��������16��3=48������Ϊa���߶Σ�
��3����a=-1+3=2���루2���ó��𰸼��ɣ�
��4�������ϵļ�����ɵó��𰸼��ɣ�
��� �⣺��1����ͼ�������εı߳�Ϊa����Ҫ�߳�Ϊa��С������1����
ͼ�������εı߳�Ϊ2a����Ҫ�߳�Ϊa��С������1+3=4����
ͼ�������εı߳�Ϊ3a����Ҫ�߳�Ϊa��С������1+3+5=9����
��
ͼn�����εı߳�Ϊna����Ҫ�߳�Ϊa��С������1+3+5+��+2n-1=n2����
Ҫʹƴ�ɵĴ������εı߳�Ϊ5a������Ҫ25���߳�Ϊa��С��������ƴ��
��2��ͼ���й���3����1+3+5+7��=48������Ϊa���߶Σ�
��3����a=-1+3=2ʱ��ͼ���г���Ϊa���߶�֮����48��2=96��
��4��ͼn����Ҫ�߳�Ϊa��С������1+3+5+��+2n-1=n2�������г���Ϊa���߶ζ���3n2����
�ʴ�Ϊ��25��48��96��3n2��
���� ���⿼��ͼ�εı仯���ɣ��ҳ�ͼ��֮�����ϵ���ó�������ɽ�����⣮


 �п�������㾫��ϵ�д�
�п�������㾫��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
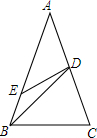 ��֪���ڡ�ABC�У�AB=AC����D��E�ֱ�����AC��AB�ϣ���BD=BC��BE=DE=AD�����C�Ķ�����
��֪���ڡ�ABC�У�AB=AC����D��E�ֱ�����AC��AB�ϣ���BD=BC��BE=DE=AD�����C�Ķ������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
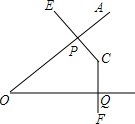 ��ͼ����֪��AOB������CE��OA�ڵ�P��CF��OB�ڵ�Q��
��ͼ����֪��AOB������CE��OA�ڵ�P��CF��OB�ڵ�Q���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3.95��102 | B�� | 0.395��103 | C�� | 3.95��103 | D�� | 395��10 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com