
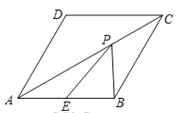
【题目】如图,在菱形![]() 中,
中,![]() =120°,点E是边
=120°,点E是边![]() 的中点,P是对角线
的中点,P是对角线![]() 上的一个动点,若AB=2,则PB+PE的最小值是( )
上的一个动点,若AB=2,则PB+PE的最小值是( )
A. 1B. ![]() C. 2D.
C. 2D. ![]()
科目:初中数学 来源: 题型:
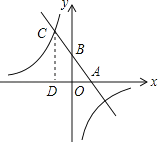
【题目】已知,如图,一次函数y=kx+b(k、b为常数,k≠0)的图象与x轴、y轴分别交于A、B两点,且与反比例函数y=![]() (n为常数且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂直为D,若OB=2OA=3OD=6.
(n为常数且n≠0)的图象在第二象限交于点C.CD⊥x轴,垂直为D,若OB=2OA=3OD=6.
(1)求一次函数与反比例函数的解析式;
(2)求两函数图象的另一个交点坐标;
(3)直接写出不等式;kx+b≤![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,二次函数y=ax2+bx+c的图象开口向上,图象经过点(﹣1,2)和(1,0),且与y轴交于负半轴,给出六个结论:①a>0;②b>0;③c>0;④a+b+c=0;⑤b2﹣4ac>0;⑥2a﹣b>0,其中正确结论序号是_____.
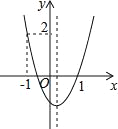
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=5,CB=8,分别以AB、AC为直径作半圆,则图中阴影部分面积是( )
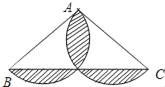
A. ![]() -24 B. 25π﹣24 C. 25π﹣12 D.
-24 B. 25π﹣24 C. 25π﹣12 D. ![]() -12
-12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在锐角三角形ABC中,点D、E分别在边AC、AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.
(1)求证:△ADE∽△ABC;
(2)若AD=BE=4,AE=3,求CD的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,在面积为3的正方形ABCD中,E、F分别是BC和CD边上的两点,AE⊥BF于点G,且BE=1.
(1)求证:△ABE≌△BCF;
(2)求出△ABE和△BCF重叠部分(即△BEG)的面积;
(3)现将△ABE绕点A逆时针方向旋转到△AB′E′(如图2),使点E落在CD边上的点E′处,问△ABE在旋转前后与△BCF重叠部分的面积是否发生了变化?请说明理由.
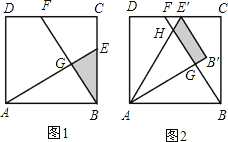
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A、B、C三点在数轴上的位置如图所示,它们表示的数分别是a、b、c
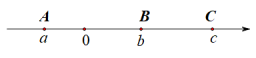
(1) 填空:abc________0,a+b________ac,ab-ac________0;(填“>”,“=”或“<”)
(2) 若|a|=2,且点B到点A、C的距离相等
① 当b2=16时,求c的值
② 求b、c之间的数量关系
③ P是数轴上B,C两点之间的一个动点设点P表示的数为x.当P点在运动过程中,bx+cx+|x-c|-10|x+a|的值保持不变,求b的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,AB=1,∠A=60°,EFGH是矩形,矩形的顶点都在菱形的边上.设AE=AH=x(0<x<1),矩形的面积为S.
(1)求S关于x的函数解析式;
(2)当EFGH是正方形时,求S的值.
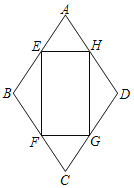
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com