
【题目】如图,一条直线上有两只蚂蚁,甲蚂蚁在点A处,乙蚂蚁在点B处,假设两只蚂蚁同时出发,爬行方向只能沿直线AB在“向左”或“向右”中随机选择,并且甲蚂蚁爬行的速度比乙蚂蚁快.(1)甲蚂蚁选择“向左”爬行的概率为________;
(2)利用列表或画树状图的方法求两只蚂蚁开始爬行后会“触碰到”的概率.
![]()
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)根据概率的求法,找准两点:①全部等可能情况的总数;②符合条件的情况数目;二者的比值就是其发生的概率.因此,由爬行方向只能沿直线AB在“向左”或“向右”中随机选择,直接利用概率公式求解即可求得答案.
(2)根据题意画出树状图或列表,然后由图表求得所有等可能的结果与两只蚂蚁开始爬行后会“触碰到”的情况,再利用概率公式即可求得答案.
试题解析:解:(1)∵爬行方向只能沿直线AB在“向左”或“向右”中随机选择,
∴甲蚂蚁选择“向左”爬行的概率为:![]() .
.
(2)画树状图得:
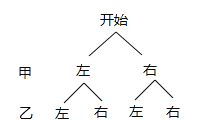
∵共有4种情况,由于甲蚂蚁爬行的速度比乙蚂蚁快,两只蚂蚁开始爬行后会“触碰到”的2种情况:甲向右乙向右,甲向右乙向左,
∴两只蚂蚁开始爬行后会“触碰到”的概率为:![]() .
.


科目:初中数学 来源: 题型:
【题目】已知:用3辆A型车和1辆B型车装满货物一次可运货13吨;用1辆A型车和2辆B型车装满货物一次可运货11吨.某物流公司现有35吨货物,计划同时租用A型车![]() 辆,B型车
辆,B型车![]() 辆,一次运完,且恰好每辆车都装满货物.
辆,一次运完,且恰好每辆车都装满货物.
根据以上信息,解答下列问题:
(1)1辆A型车和1辆B型车都装满货物一次可分别运货多少吨?
(2)请你帮该物流公司设计租车方案;
(3)若A型车每辆需租金100元/次,B型车每辆需租金120元/次.请选出最省钱的租车方案,并求出最少租车费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系中的任意两点P1(x1,y1),P2(x2,y2),我们把|x1-x2|+|y1-y2|叫做P1、P2两点间的直角距离,记作d(P1,P2).
(1) 令P0(2,-3),O为坐标原点,则d(O,P0)= ;
(2)已知O为坐标原点,动点P(x,y)满足d(O,P)=1,请写出x与y之间满足的关系式,并在所给的直角坐标系中画出所有符合条件的点P所组成的图形;
(3)设P0(x0,y0)是一定点,Q(x,y)是直线y=ax+b上的动点,我们把d(P0,Q)的最小值叫做P0到直线y=ax+b的直角距离. 若P(a,-3)到直线y=x+1的直角距离为6,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个质地均匀的正四面体的四个面上依次标有数字-2,0,1,2,连续抛掷两次,朝下一面的数字分别是a,b,将其作为M点的横、纵坐标,则点M(a,b)落在以A(-2,0),B(2,0),C(0,2)为顶点的三角形内(包含边界)的概率是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小晗家客厅装有一种三位单极开关,分别控制着A(楼梯)、B(客厅)、C(走廊)三盏电灯,在正常情况下,小晗按下任意一个开关均可打开对应的一盏电灯,既可三盏、两盏齐开,也可分别单盏开.因刚搬进新房不久,不熟悉情况.
(1)若小晗任意按下一个开关,正好楼梯灯亮的概率是多少?
(2)若任意按下一个开关后,再按下另两个开关中的一个,则正好客厅灯和走廊灯同时亮的概率是多少?请用树状图或列表法加以说明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,己知△ABC是等边三角形,点P在△ABC内,点Q在△ABC外,分别连接AP、BP、AQ、CQ,∠ABP=∠ACQ, BP=CQ.
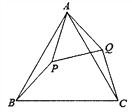
(1)求证:△ABP≌△ACQ;
(2)连接PQ,求证△APQ是等边三角形;
(3)连接P设△CPQ是以![]() PQC为顶角的等腰三角形,且∠BPC=100
PQC为顶角的等腰三角形,且∠BPC=100![]() ,求∠APB的度数.
,求∠APB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠A=36°,DE是AC的垂直平分线.

(1)求证:△BCD是等腰三角形;
(2)△BCD的周长是a,BC=b,求△ACD的周长(用含a,b的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某农民在自己家承包的甲、乙两片荒山上各栽了200棵苹果树,成活率均为96%,现已挂果.他随意从甲山采摘了4棵树上的苹果,称得质量(单位:千克)分别为36,40,48,36;从乙山采摘了4棵树上的苹果,称得质量(单位:千克)分别为50,36,40,34,将这两组数据组成一个样本,回答下列问题:
(1)样本容量是多少?
(2)样本平均数是多少?并估算出甲、乙两山苹果的总产量;
(3)甲、乙两山哪个山上的苹果长势较整齐?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一块铁皮,拱形边缘呈抛物线状,MN=4,抛物线顶点处到边MN的距离是4,要在铁皮上截下一矩形ABCD,使矩形顶点B、C落在边MN上,A、D落在抛物线上.
(1)如图建立适当的坐标系,求抛物线解析式;
(2)设矩形ABCD的周长为L,点C的坐标为(m,0),求L与m的关系式(不要求写自变量取值范围).
(3)问这样截下去的矩形铁皮的周长能否等于9.5,若不等于9.5,请说明理由,若等于9.5,求出吗的值?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com