
【题目】问题探究
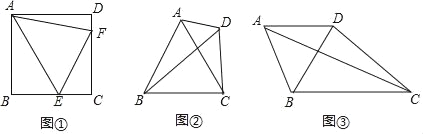
(1)如图①,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,则线段BE、EF、FD之间的数量关系为 ;
(2)如图②,在△ADC中,AD=2,CD=4,∠ADC是一个不固定的角,以AC为边向△ADC的另一侧作等边△ABC,连接BD,则BD的长是否存在最大值?若存在,请求出其最大值;若不存在,请说明理由;
问题解决
(3)如图③,在四边形ABCD中,AB=AD,∠BAD=60°,BC=4![]() ,若BD⊥CD,垂足为点D,则对角线AC的长是否存在最大值?若存在,请求出其最大值;若不存在,请说明理由.
,若BD⊥CD,垂足为点D,则对角线AC的长是否存在最大值?若存在,请求出其最大值;若不存在,请说明理由.
【答案】(1)BE+DF=EF;(2)存在,BD的最大值为6;(3)存在,AC的最大值为2![]() +2
+2![]() .
.
【解析】
(1)作辅助线,首先证明△ABE≌△ADG,再证明△AEF≌△AEG,进而得到EF=FG问题即可解决;
(2)将△ABD绕着点B顺时针旋转60°,得到△BCE,连接DE,由旋转可得,CE=AD=2,BD=BE,∠DBE=60°,可得DE=BD,根据DE<DC+CE,则当D、C、E三点共线时,DE存在最大值,问题即可解决;
(3)以BC为边作等边三角形BCE,过点E作EF⊥BC于点F,连接DE,由旋转的性质得△DBE是等边三角形,则DE=AC,根据在等边三角形BCE中,EF⊥BC,可求出BF,EF,以BC为直径作⊙F,则点D在⊙F上,连接DF,可求出DF,则AC=DE≤DF+EF,代入数值即可解决问题.
(1)如图①,延长CD至G,使得DG=BE,
∵正方形ABCD中,AB=AD,∠B=∠AFG=90°,
∴△ABE≌△ADG,
∴AE=AG,∠BAE=∠DAG,
∵∠EAF=45°,∠BAD=90°,
∴∠BAE+∠DAF=45°,
∴∠DAG+∠DAF=45°,即∠GAF=∠EAF,
又∵AF=AF,
∴△AEF≌△AEG,
∴EF=GF=DG+DF=BE+DF,
故答案为:BE+DF=EF;
(2)存在.
在等边三角形ABC中,AB=BC,∠ABC=60°,
如图②,将△ABD绕着点B顺时针旋转60°,得到△BCE,连接DE.
由旋转可得,CE=AD=2,BD=BE,∠DBE=60°,
∴△DBE是等边三角形,
∴DE=BD,
∴在△DCE中,DE<DC+CE=4+2=6,
∴当D、C、E三点共线时,DE存在最大值,且最大值为6,
∴BD的最大值为6;
(3)存在.
如图③,以BC为边作等边三角形BCE,过点E作EF⊥BC于点F,连接DE,
∵AB=BD,∠ABC=∠DBE,BC=BE,
∴△ABC≌△DBE,
∴DE=AC,
∵在等边三角形BCE中,EF⊥BC,
∴BF=![]() BC=2
BC=2![]() ,
,
∴EF=![]() BF=
BF=![]() ×2
×2![]() =2
=2![]() ,
,
以BC为直径作⊙F,则点D在⊙F上,连接DF,
∴DF=![]() BC=
BC=![]() ×4
×4![]() =2
=2![]() ,
,
∴AC=DE≤DF+EF=2![]() +2
+2![]() ,即AC的最大值为2
,即AC的最大值为2![]() +2
+2![]() .
.


科目:初中数学 来源: 题型:
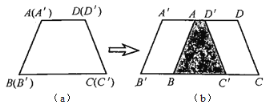
【题目】两个形状和大小完全一样的梯形纸片如图(a)所示摆放,将梯形纸片![]() 沿上底
沿上底![]() 方向向右平移得到图(b).已知
方向向右平移得到图(b).已知![]() ,
,![]() ,若阴影部分的面积是四边形
,若阴影部分的面积是四边形![]() 的面积的
的面积的![]() .则图(b)中平移距离为____.
.则图(b)中平移距离为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交BC,AC于点D,E,DG⊥AC于点G,交AB的延长线于点F.
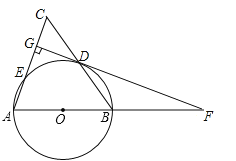
(1)求证:直线FG是⊙O的切线;
(2)若AC=10,cosA=![]() ,求CG的长.
,求CG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
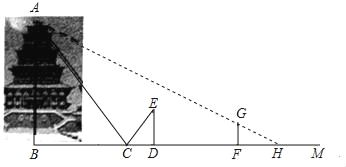
【题目】我市某学校在“行读石鼓阁”研学活动中,参观了我市中华石鼓园,石鼓阁是宝鸡城市新地标.建筑面积7200平方米,为我国西北第一高阁.秦汉高台门阙的建筑风格,追求稳定之中的飞扬灵动,深厚之中的巧妙组合,使景观功能和标志功能融为一体.小亮想知道石鼓阁的高是多少,他和同学李梅对石鼓阁进行测量.测量方案如下:如图,李梅在小亮和“石鼓阁”之间的直线BM上平放一平面镜,在镜面上做了一个标记,这个标记在直线BM上的对应位置为点C,镜子不动,李梅看着镜面上的标记,她来回走动,走到点D时,看到“石鼓阁”顶端点A在镜面中的像与镜面上的标记重合,这时,测得李梅眼睛与地面的高度ED=1.6米,CD=2.2米,然后,在阳光下,小亮从D点沿DM方向走了29.4米,此时“石鼓阁”影子与小亮的影子顶端恰好重合,测得小亮身高1.7米,影长FH=3.4米.已知AB⊥BM,ED⊥BM,GF⊥BM,其中,测量时所使用的平面镜的厚度忽略不计,请你根据题中提供的相关信息,求出“石鼓阁”的高AB的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段AE上一动点(不与A、E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ,以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤∠AOB=60°其中完全正确的是( )
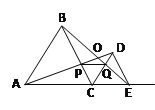
A.①②③④B.②③④⑤C.①③④⑤D.①②③⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】充实而快乐的暑假生活即将结束,校学生会张同学采用随机抽样的方式对初三年级学生暑期生活进行了问卷调查,并将调查结果按照“A社会实践类、B学习提高类、C游艺娱乐类、D其他”进行了分类统计,绘制了如图1和如图2两幅不完整的统计图.(接受调查的每名同学只能在四类中选择其中一种类型,不可多选或不选)请根据图中提供的信息完成以下问题:
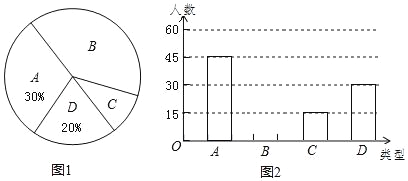
(1)扇形统计图中表示B类的扇形圆心角是 度,并补全条形统计图;
(2)张同学已从被调查的同学中确定了4名同学进行开学后的经验交流,其中A社会实践类1人,B学习提高类3人,并计划在这四人中选出两人的宝贵经验刊登在校刊上.请利用画树状图或列表的方法求出选出的恰好是A、B类各一人的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)等腰三角形底边长为6cm,一腰上的中线把它的周长分成两部分的差为2cm,则腰长为________.
(2)已知![]() 的周长为24,
的周长为24,![]() ,
,![]() 于点D,若
于点D,若![]() 的周长为20,则AD的长为________.
的周长为20,则AD的长为________.
(3)已知等腰三角形的周长为24,腰长为x,则x的取值范围是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ΔABC中,AB=AC,∠A=40O,延长AC到D,使CD=BC,点P是ΔABD的内心,则∠BPC=
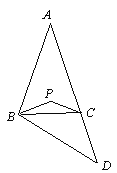
A. 105° B. 110° C. 130° D. 145°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CD是⊙O的直径,AB,EF是⊙O的弦,且AB∥CD∥EF,AB=16,CD=20,EF=12,则图中阴影部分的面积是( )
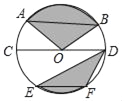
A. 96+25π B. 88+50π C. 50π D. 25π
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com