
【题目】(12分)如图,在△ABC中,AB=AC,以AB为直径的⊙O分别交BC,AC于点D,E,DG⊥AC于点G,交AB的延长线于点F.
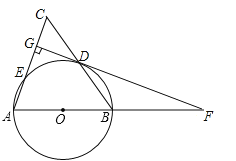
(1)求证:直线FG是⊙O的切线;
(2)若AC=10,cosA=![]() ,求CG的长.
,求CG的长.
【答案】(1)证明见试题解析;(2)3.
【解析】
试题分析:(1)先得出OD∥AC,有∠ODG=∠DGC,再由DG⊥AC,得到∠DGC=90°,∠ODG=90°,得出OD⊥FG,即可得出直线FG是⊙O的切线.
(2)先得出△ODF∽△AGF,再由cosA=![]() ,得出cos∠DOF=
,得出cos∠DOF=![]() ;然后求出OF、AF的值,即可求出AG、CG的值.
;然后求出OF、AF的值,即可求出AG、CG的值.
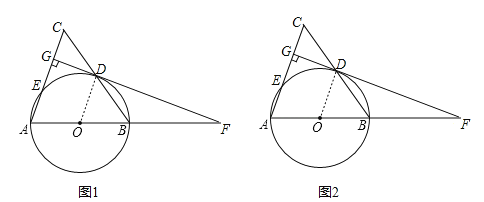
试题解析:(1)如图1,连接OD,∵AB=AC,∴∠C=∠ABC,∵OD=OB,∴∠ABC=∠ODB,∴∠ODB=∠C,∴OD∥AC,∴∠ODG=∠DGC,∵DG⊥AC,∴∠DGC=90°,∴∠ODG=90°,∴OD⊥FG,∵OD是⊙O的半径,∴直线FG是⊙O的切线;
(2)如图2,∵AB=AC=10,AB是⊙O的直径,∴OA=OD=10÷2=5,由(1),可得:OD⊥FG,OD∥AC,∴∠ODF=90°,∠DOF=∠A,在△ODF和△AGF中,∵∠DOF=∠A,∠F=∠F,∴△ODF∽△AGF,∴![]() ,∵cosA=
,∵cosA=![]() ,∴cos∠DOF=
,∴cos∠DOF=![]() ,∴OF=
,∴OF=![]() =
=![]() =
=![]() ,∴AF=AO+OF=
,∴AF=AO+OF=![]() =
=![]() ,∴
,∴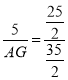 ,解得AG=7,∴CG=AC﹣AG=10﹣7=3,即CG的长是3.
,解得AG=7,∴CG=AC﹣AG=10﹣7=3,即CG的长是3.


科目:初中数学 来源: 题型:
【题目】如图,在长方形ABCD中,AB=10厘米,BC=6厘米,点P沿AB边从点A开始向点B以3厘米/秒的速度移动;点Q沿DA边从点D开始向点A以2厘米/秒的速度移动.如果P、Q同时出发,用t (秒)表示移动的时间,那么:
(1)如图1,用含t的代数式表示AP= ,AQ= .并求出当t为何值时线段AP=AQ.
(2)如图2,在不考虑点P的情况下,连接QB,问:当t为何值时△QAB的面积等于长方形面积的![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件是必然事件的是( )
A.经过不断的努力,每个人都能获得“星光大道”年度总冠军
B.小冉打开电视,正在播放“奔跑吧,兄弟”
C.火车开到月球上
D.在十三名中国学生中,必有属相相同的
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级有15名同学参加校运会百米比赛,预赛成绩各不相同,前7名才有资格参加决赛,小明已经知道了自己的成绩,但他想知道自己能否进入决赛,还需要知道这15名同学成绩的_____.(填“极差”、“众数”或“中位数”)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】买一个足球需要m元,买一个篮球需要n元,则买4个足球、7个篮球共需( )
A.28mn 元 B.11mn元 C.(7m+4n)元 D.(4m+7n)元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】王华、张伟两位同学分别将自己10次数学自我检测的成绩绘制成如下统计图:
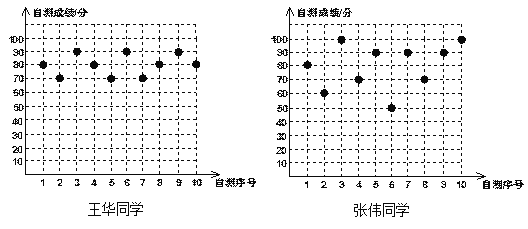
(1)根据上图中提供的数据列出如下统计表:
平均成绩(分) | 中位数(分) | 众数(分) | 方差(S2) | |
王华 | 80 | b | 80 | d |
张伟 | a | 85 | c | 260 |
则a= ,b= ,c= ,d= ,
(2)将90分以上(含90分)的成绩视为优秀,则优秀率高的是 .
(3)现在要从这两个同学选一位去参加数学竞赛,你可以根据以上的数据给老师哪些建议?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com