
【题目】如图,抛物线y=x2+bx+c与直线y=![]() x-3交于A,B两点,其中点B在y轴上,点A坐标为(-4,-5),点P为y轴左侧的抛物线上一动点,过点P作PC⊥x轴于点C,交AB于点D.
x-3交于A,B两点,其中点B在y轴上,点A坐标为(-4,-5),点P为y轴左侧的抛物线上一动点,过点P作PC⊥x轴于点C,交AB于点D.
(1)求抛物线的解析式;
(2)以O,B,P,D为顶点的平行四边形是否存在?如存在,求点P的坐标;若不存在,说明理由;
(3)当点P运动到直线AB下方某一处时,△PAB的面积是否有最大值?如果有,请求出此时点P的坐标.

【答案】(1)y=x2+![]() x-3(2)存在,(-2-
x-3(2)存在,(-2-![]() ,-1-
,-1-![]() ),(-1,-
),(-1,-![]() ),(-3,-
),(-3,-![]() )(3)(-2,-8)
)(3)(-2,-8)
【解析】
(1)由题意可得点B(0,-3),将点B,点A坐标代入解析式,可求抛物线解析式;
(2)设P(m,m2+![]() m-3),则点D(m,
m-3),则点D(m,![]() m-3),可得PD=|m2+4m|,以O,B,P,D为顶点的平行四边形且OB∥PD,可得PD=|m2+4m|=OB=3,可求m的值,即可得点P的坐标;
m-3),可得PD=|m2+4m|,以O,B,P,D为顶点的平行四边形且OB∥PD,可得PD=|m2+4m|=OB=3,可求m的值,即可得点P的坐标;
(3)设点P(x,x2+![]() x-3),则点D(x,
x-3),则点D(x,![]() x-3),则PD=-x2-4x,由题意可得S△PAB=
x-3),则PD=-x2-4x,由题意可得S△PAB=![]() ×PD×4,根据二次函数的性质,可求△PAB的面积的最大值.
×PD×4,根据二次函数的性质,可求△PAB的面积的最大值.
(1)∵直线y=![]() x-3交y轴于点B
x-3交y轴于点B
∴B(0,-3),
∵抛物线y=x2+bx+c经过点A(-4,-5),点B(0,-3)
∴![]()
解得:b=![]() ,c=-3
,c=-3
∴抛物线解析式y=x2+![]() x-3
x-3
(2)存在,
设P(m,m2+![]() m-3),(m<0),
m-3),(m<0),
∴D(m,![]() m-3),
m-3),
∴PD=|m2+4m|
∵PD∥BO,
∴当PD=OB=3,故存在以O,B,P,D为顶点的平行四边形,
∴|m2+4m|=3,
①当m2+4m=3时,
∴m1=-2-![]() ,m2=-2+
,m2=-2+![]() (舍),
(舍),
当m=-2-![]() 时,则m2+
时,则m2+![]() m-3=-1-
m-3=-1-![]()
∴P(-2-![]() ,-1-
,-1-![]() ),
),
②当m2+4m=-3时,
∴m1=-1,m2=-3,
当m1=-1时,则m2+![]() m-3=-
m-3=-![]() ,
,
∴P(-1,-![]() ),
),
当m2=-3,∴m2+![]() m-3=-
m-3=-![]() ,
,
∴P(-3,-![]() ),
),
∴点P的坐标为(-2-![]() ,-1-
,-1-![]() ),(-1,-
),(-1,-![]() ),(-3,-
),(-3,-![]() ).
).
(3)设点P(x,x2+![]() x-3),则点D(x,
x-3),则点D(x,![]() x-3),
x-3),
∴PD=![]() x-3-(x2+
x-3-(x2+![]() x-3)=-x2-4x
x-3)=-x2-4x
∵S△APB=![]() ×PD×4=-2x2-8x=-2(x+2)2+8
×PD×4=-2x2-8x=-2(x+2)2+8
∴当x=-2时,△PAB的面积的最大值为8.
∴点P坐标(-2,-8)


 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
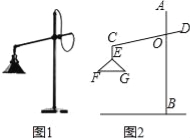
【题目】如图1所示的是一种置于桌面上的简易台灯,将其结构简化成图2,灯杆AB与CD交于点O(点O固定),灯罩连杆CE始终保持与AB平行,灯罩下方FG处于水平位置,测得OC=20cm,∠COB=70°,∠F=40°,EF=EG,点G到OB的距离为12cm.
(1)求∠CEG的度数.
(2)求灯罩的宽度(FG的长;结果精确到0.1cm,可用科学计算器).
(参考数据:sin40°≈0.643,cos40°≈0.766,sin70°≈0.940,cos70°≈0.342)
查看答案和解析>>
科目:初中数学 来源: 题型:
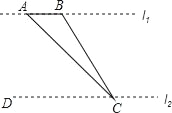
【题目】如图,某数学兴趣小组为了测量河对岸l1的两棵古树A、B之间的距离,他们在河这边沿着与AB平行的直线l2上取C、D两点,测得∠ACB=15°,∠ACD=45°,若l1、l2之间的距离为50m,则古树A、B之间的距离为_____m.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系内,△ABC各顶点的坐标分别是A(﹣2,4),B(﹣4,3),C(﹣1,1).将△ABC向右平移5个单位长度,再向下平移4个单位长度得到△A′B′C′.
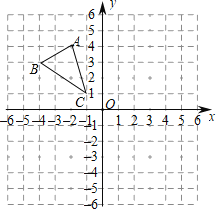
(1)请作出平移后的△A′B′C′,并写出△A′B′C′各顶点的坐标;
(2)如果将△A′B′C′看成是由△ABC经过一次平移得到的,请指出这一平移的平移方向和平移距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
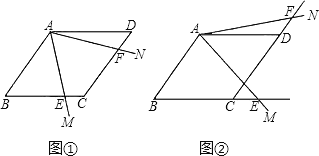
【题目】如图,菱形ABCD中,∠ABC=60°,有一度数为60°的∠MAN绕点A旋转.
(1)如图①,若∠MAN的两边AM,AN分别交BC,CD于点E,F,则线段CE,DF的大小关系如何?请证明你的结论;
(2)如图②,若∠MAN的两边AM,AN分别交BC,CD的延长线于点E,F,猜想线段CE,DF的大小关系如何?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=3,CD=4,点P是AC上一个动点(点P与点A,C不重合),过点P分别作PE⊥BC于点E,PF∥BC交AB于点F,连接EF,则EF的最小值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
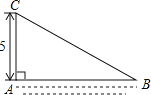
【题目】如图所示,在离水面高度5米的岸上有人用绳子拉船靠岸,开始时绳子BC的长度为13米,此人以每秒0.5米的速度收绳.问:
(1)未开始收绳的时候,图中船B距岸A的长度AB是多少米?
(2)收绳10秒后船向岸边移动了多少米?(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为宣传“扫黑除恶”专项行动,社区准备制作一幅宣传版面,喷绘时为了美观,要在矩形图案四周外围增加一圈等宽的白边,已知图案的长为2米,宽为1米,图案面积占整幅宣传版面面积的90%,若设白边的宽为x米,则根据题意可列出方程( )

A. 90%×(2+x)(1+x)=2×1 B. 90%×(2+2x)(1+2x)=2×1
C. 90%×(2﹣2x)(1﹣2x)=2×1 D. (2+2x)(1+2x)=2×1×90%
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△DEB中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是

A.BC=EC,∠B=∠E B.BC=EC,AC=DC
C.BC=DC,∠A=∠D D.∠B=∠E,∠A=∠D
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com